Fisica Terrestre Parte 5 - Dipartimento di Geoscienze

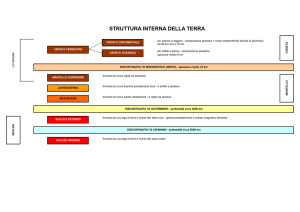
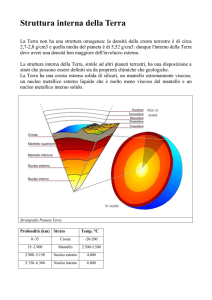
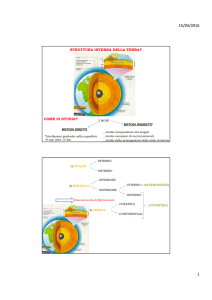
Fisica Terrestre Parte V
Geotermia
A. Caporali
Dipartimento di Geologia, Paleontologia e Geofisica
Università di Padova
Flusso Termico
Secondo principio della Termodinamica: il calore fluisce da un corpo caldo verso uno freddo
Temperatura: va intesa come energia cinetica media di molecole all’interno di un dato
volume
Possibili modi di trasmissione del calore:
Conduzione: le molecole si trasmettono s’una con l’altra l’energia vibrazionale. Non c’e’
trasporto di massa; pertanto la conduzione è tipica nei solidi (ad es. crosta)
Convezione: le molecole in stato di maggiore eccitazione si spostano collettivamente
da un punto all’altro. Pertanto la convezione è tipica nei fluidi (ad es. mantello)
Radiazione: l’energia viene irradiata dalle molecole sotto forma di onde
elettromagnetiche (in particolare nell’infrarosso). Pertanto la radiazione è tipica nei gas
(ad es. aria)
Relazione Flusso di calore – gradiente di temperatura:
q( z )  k
T
z
T
dz
Il segno meno è dovuto al fatto che Q aumenta nella direzione in cui T diminuisce.
La costante k è detta costante di conducibilità termica.
q si misura in W/m2; T in gradi Kelvin (K)
q
Dati numerici sul flusso termico
In cave o miniere si trova dT/dz~20-30deg/km
In laboratorio si determina per rocce superficiali k ~ 2-3 W/K*m
Si conclude che in superficie q~40-90 mW/m2
Dati più accurati si ottengono calando un termistor in un pozzo a 300-400 m, per rimuovere
gli effetti stagionali
+10% in Africa
Flusso termico della Terra
Nei Continenti (Area=2*108 km2) qcontin=56.5 mW/m2
Negli Oceani (Area=3.1*108 km2) qoceani=78.2 mW/m2
-10% in Australia
+15% in N Pacifico
-15% in S Atlantico
Nei continenti il Flusso Termico è fortemente correlato con la concentrazione dei
radioisotopi ed è invers. proporzionale all’età delle rocce superficiali
Negli oceani il Flusso Termico è correlato con l’età delle rocce ( distanza dal ridge). La
concentrazione dei radioisotopi è ininfluente anche perché solo il 2% di quella nei continenti
Flusso totale terrestre= media pesata continenti + oceani:
56.5*(2/5.1)+78.2*(3.1/5.1)=70 mW/m2
Equazione della conduzione, o di Fourier
Caso stazionario (steady state): dato un volume limitato da una base di area a e altezza dz,
contenente una sorgente di calore Hradz Watt, il flusso termico uscente per la faccia
superiore è uguale al flusso termico entrante per la faccia inferiore + il calore generato
internamente, ed è indipendente da a:
q(z)
dq
 Hr
dz
H  quantità di calore prodotto dall' unità di massa
q( z  dz )  q( z )  Hrdz 
Pertanto in condizioni stazionarie (la temperatura del corpo è costante nel tempo)
q( z )
 2T
 Hr  k 2  Hr  0
z
z
rH
q(z+dz)
Equazione di Fourier nel caso non stazionario
Caso non stazionario: in conseguenza della generazione interna di calore e del flusso di calore tra le
due pareti, la temperatura del corpo varia nel tempo. In tal caso, detto cp il calore specifico,
cioè la quantità di calore necessaria per innalzare la temperatura di 1 kg di 1 C, e r la densità,
la differenza tra i due termini sopra, uguali nel caso steady state, è esattamente la quantità di
calore necessaria per far variare la temperatura nel tempo:
T
 2T
c p rdz
 (k 2  rH )dz
t
z
Il termine Hr è per la Terra di natura radioattiva (Uranio, Torio e Potassio), concentrati
prevalentemente nella crosta e, in misura minore, nel mantello. Tuttavia il contributo del
mantello alla quantità di calore complessivamente prodotto dalla Terra è maggiore di quello
della crosta, a causa del maggiore volume del mantello rispetto alla crosta.
Complessivamente il calore prodotto internamente dalla Terra e dissipato verso l’esterno è 4
1013 W (pari a 8 10-2 W m-2, essendo 4pR2 ~ 2 1015 m2 l’area della superficie
Terrestre).Questo flusso di calore è solo 1/10000 del flusso di calore radiato dalla Terra verso
l’esterno. Il maggior contributo viene dalla luce solare riflessa dalla superficie terrestre e
dall’atmosfera.
Geoterma stazionaria con concentrazione di
radioisotopi costante
L’equazione da risolvere è:
 2T
k 2  Hr  0 geoterma stazionari a
z
Hr  cost
E’ una eq. del second’ordine  devo assegnare due condizioni iniziali, ad
es. la T in superfice Ts=T(0) e il flusso termico in superfice qs=q(0), che
sono entrambi misurabili sperimentalmente. L’integrale generale è:
T ( z)  
1 Hr 2
z  c1 z  c2
2 k
Le costanti c1, c2 vengono determinate imponendo
le condizioni al contorno a z=0 (cioè in superficie):
La soluzione che soddisfa le condizioni al
contorno è dunque:
qs
c2  Ts c1  
k
T ( z)  
1 Hr 2 qs z
z 
 Ts
2 k
k
Esempi di geoterma stazionaria a
concentrazione costante
Legenda:
a) k=2.5 W/m/C,
Hr=1.25mW/m3;
qs=0.021W/m2, Ts=0
c) Come a) eccetto
Hr=2.5mW/m3
e) Come a) eccetto
qs=0.0105W/m2
Geoterma stazionaria della crosta continentale (1/2)
Si osservano forti deviazioni dall’andamento quadratico
Per il granito in superficie Hcrosta=9.6 10-10 W/kg
Posto hcrosta=35 km, rcrosta=2700 kg/m3 si ottiene
qcrosta= (rHh) crosta=91 mW/m2 >> qmedio=56.5 mW/m2
Concludiamo che su scala crostale la concentrazione di
radioisotopi non può essere considerata costante bensì
decrescente con la profondità.
Modello empirico : rH(z)=rHse-z/hr ove hr è un fattore di scala da
determinarsi sperimentalmente come segue:
Geoterma stazionaria della crosta continentale (2/2)
Integro l’equazione differenziale della geoterma stazionaria tra z=z e z=infinito (corrisponde a
grandi profondità, diciamo la base della litosfera)
rH s
d T


e
2
dz
k
2

z
hr

dT dT

dz dz
 q( z )  qmantello( z  )  rH s hr e

rH s hr
k
z 


e
z zz
hr
z 
z
hr
In superficie (z  0) : qs  q(0)  qmantello( z  )  rH s hr
qs e rHs possono essere misurati in punti diversi in una data area geografica. Si ottiene
una retta di pendenza hr e intercetta qm. Valori tipici sono hr~7.5 km, qm~30 mW/m2
(flusso termico ridotto al mantello). Una successiva integrazione tra 0 (superficie) e z dà
la geoterma (NB: qm ha il segno + perché trattasi di flusso
entrante nella crosta dal
zz
z
mantello):
qm z rH s hr2  hr
T ( z )  Ts 

e
k
k
z 0

qm z rH s hr2 
T ( z )  Ts 

1  e hr
k
k 
z




Effetto in profondità di variazioni periodiche
della temperatura in superficie(1/2)
Ricerca della soluzione della equazione della
conduzione del calore per H=0 e
T(z=0,t)=T0+DTcoswt
Si dimostra che la soluzione che soddisfa alle
condizioni al contorno a) andamento sinusoidale a
z=0, b) T=0 per z=infinito è del tipo:
T ( z, t )  T0  DTe

z
L
  2T 
T
cp r
 k  2 
t
 z 
z
2k
cos(wt  ) con L 
L
wrc p
L viene chiamata skin depth (spessore della pelle). Per valori di cp, r e k tipici delle rocce superficiali, L è di
qualche decimetro per variazioni diurne di temperatura, di qualche metro per variazioni annuali e di qualche
km per variazioni su scala dei periodi glaciali (0.1Ma). Ne segue che le variazioni di temperatura superficiale
dovute alle glaciazioni non possono essere ignorate nel calcolo della geoterma in profondità. Si noti lo
sfasamento della risposta, all’aumentare della profondità.
Effetto in profondità di variazioni periodiche
della temperatura in superficie(2/2)
Esempio della attenuazione in ampiezza e
dello sfasamento all’aumentare della
profondità.
Nota: k=k/rcp è il coefficiente di diffusione
(tipicamente 1 mm2/sec).
Per una glaciazione di 10.000 anni (104 anni),
la skin depth è 317 m. Se dunque si vuole
conoscere a quale profondità l’effetto
periodico dei cicli glaciali in superfice è ridotto
al 5% dell’ampiezza in superifice, si imporrà
DTe-z/317=0.05DT, ovvero z=950 m.
Riscaldamento istantaneo di un semispazio
cp r
  2T 
T
 k  2 
t
 z 
Condizioni al contorno:
T=T0 per y>0, t=0T=Ts per y=0 , t=0+
TT0 per yinfinito, t>0
Soluzione dell’equazione della conduzione di
calore
T  T0
z
 erfc ) ove si è posto  
Ts  T0
2 kt
Ove è stata introdotta la funzione di errore
complementare:
erfc( z )  1 
2
p
z
z'
e
 dz'
2
0
Raffreddamento istantaneo di un semispazio
T0
cp r
Ts
T
  2T 
T
 k  2 
t
 z 
Condizioni al contorno:
T=T0 per y>0, t=0T=Ts per y=0 , t=0+
TT0 per yinfinito, t>0
Soluzione dell’equazione della conduzione di
calore
T  Ts
z
 erfc ) ove si è posto  
T0  Ts
2 kt
t = 0-
t = 0+
t >0
Se in superficie la temperatura cresce di 10°,dopo quanto tempo la
temperatura cresce di 1° a 3 m di profondità? Si assuma k=1 mm2/s
T  T0
z
 erfc ) ove si è posto  
Ts  T0
2 kt
T  T0
1

 0.1  erfc(1.13)
Ts  T0 10
z
2 kt

 1.13  t 
z2
4 * 2 * k
9
 1.96 *10^6 sec  20 giorni
4 * (1.13) 2 * (0.001) 2
eta
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
erfc(eta)
1.00
0.89
0.78
0.67
0.57
0.48
0.40
0.32
0.26
0.20
0.16
0.12
0.09
0.07
0.05
0.03
0.02
0.02
0.01
0.01
0.00
Riscaldamento di un semispazio per
variazione istantanea di flusso di calore
Il flusso di calore q soddisfa la stessa eq.ne di Fourier della Temperatura T:
  2T 
T
 k  2 
t
 z 
T
q  k
z
q0
cpr
 cp r
qs
q
  2q 
q
 k  2 
t
 z 
Condizioni al contorno:
t = 0-
q=q0 per y>0, t=0q=qs per y=0 , t=0+
qq0 per yinfinito, t>0
Soluzione dell’equazione della conduzione di
calore
q  q0erfc ) ove si è posto  
z
2 kt
t = 0+
t >0
Corrispondente variazione di temperatura, sulla
superficie e all’interno del semispazio (1/2)
Questa situazione si verifica per scorrimento sul piano di faglia (‘Frictional Heating’)
nel caso di subduzione oppure slip cosismico: Rocce a temperatura nominale T0
aumentano la loro temperatura a causa dello sviluppo di flusso termico q0 associato a
uno sforzo di taglio t (Pa)e uno slip u (m/sec): q0 =u t
z
q  q0erfc ) ove si è posto  
2 kt
q0
T
z



erfc
(
)
T

z
k
2 kt
q( z )  k
z
Integriamo questa ED, assumendo T -> T0 per z ->∞


q
q
2q kt
z'
z'
  dT   0  erfc(
)dz '  0  erfc(
)dz '  0
erfc( ' )d '

k
k
k
2
k
t
2
k
t
T0

z

T
z
Integrando per parti il secondo membro otteniamo T=T(z,t)
z
2q0 kt
2q0  kt  4kt z
 z 
T  T0 
 erfc( ' )d '  k  p e  2 erfc 2 kt 
k



2
Corrispondente variazione di temperatura, sulla
superficie e all’interno del semispazio (2/2)
La temperatura sul piano di scorrimento (z=0) è legata alla temperatura nominale T0
che si aveva a t<0, prima cioè dell’innesco
del flusso anomalo di calore q0 dalla
2
z
relazione:
2q0  kt  4kt z
 z 
T  T0 

2q0
k
e

k  p
 erfc
 
2
 2 kt  z 0
kt
p
Quindi ancora una volta la temperatura cresce con la radice del tempo contato dall’epoca alla quale
si è innescato l’aumento (o diminuzione) di flusso termico. Per applicazioni di tipo frizionale abbiamo:
q0=ut, dove t è lo sforzo di taglio sul piano di faglia e u=dx/dt la velocità di scorrimento
t=x/u, ove x è la coordinata lungo il piano di faglia, che immerge a un angolo d rispetto all’orizzontale
y=x sin d è la profondità di un punto di coordinata x
T0
2q
T  T0  0
k
kt 2tu kx 2t kux 2t
kuy



p
k pu
k
p
k p sin d
d
T
u
x
y
Profilo termico nelle rocce circostanti una faglia,
durante un terremoto
18
0.1 s
0.2 s
0.3 s
0.4 s
2
Aumento della temperatura in un semispazio con k=4 W/(m*K), kappa=1 mm /s, per un terremoto con
stress drop tau=10MPa, slip=4 m, velocità sul piano u=10 m/s . Al termine dello slip (0.4 s) la temperatura
sulla superficie di scorrimento è aumentata di 17000 K.
16
aumento di temperatura (* 1000 K)
14
12
10
8
6
4
2
0
0
1
2
3
4
5
6
distanza dalla superfice di scorrimento (m)
7
8
9
10
Riscaldamento o raffreddamento
istantaneo di un semispazio
Applicazioni tipiche del modello di raffreddamento/riscaldamento
istantaneo sono:
1.
2.
3.
Supponiamo che una porzione di spessore l della superficie terrestre
viene rimossa ‘improvvisamente’ (su scale geologiche), ad esempio
per erosione. Prima della rimozione, la geoterma era T=T0+by. Dopo
la rimozione la nuova superficie esposta ha una temperatura T=T0
costante. Determinare la nuova geoterma.
Consideriamo l’alternanza dei periodi di glaciazione come un’onda
quadra. Determinare la geoterma corrispondente.
Infine, la dislocazione di masse in faglie inverse può portare alla
sovrapposizione di masse (che in origine erano sepolte) sopra masse
che in origine erano esposte. Analogamente in faglie di
scorrimento(ad es. quelle sul fondo oceanico), semispazi a
temperature diverse possono entrare in contatto. In questi casi la
legge matematica che dà l’andamento della temperatura all’interno
dei blocchi è la stessa che nei casi precedenti.
Raffreddamento della Litosfera oceanica
~t1/2
Spessore della litosfera
(km)
La litosfera può essere pensata come la regione compresa tra la superficie a temperatura
zero e la geoterma (1600 K) oltre la quale le temperature sono sufficientemente elevate che
le rocce si deformano su tempi geologici.
Le placche di litosfera oceanica sono formate da rocce calde (a temperatura Tm)
provenienti per convezione dal mantello lungo l’asse del ridge. Queste rocce a contatto con
l’acqua degli oceani a temperatura Ts si raffreddano, formando una placca che tende ad
allontanarsi dal ridge con velocità costante u=x/t.
Lo spessore della litosfera oceanica aumenta con la separazione dal ridge, perché ha più
tempo per raffreddarsi. Aumentando di densità affonda perché diminuisce la spinta
isostatica.
In altre parole, la nostra teoria predice che la profondità della isoterma a 1600 K aumenta
con la radice quadrata della separazione dal ridge (ovvero con la radice quadrata dell’età
termica delle rocce), come dimostrato sperimentalmente:
Struttura termica della litosfera
in subduzione
Le variazioni laterali di temperatura sono strettamente correlate al trasporto di
calore e al flusso convettivo nel mantello. Il ciclo termico prevede il
sollevamento, dispersione laterale e raffreddamento di una superficie
inizialmente calda quanto il mantello, e il successivo riscaldamento della litosfera
fredda come rientra nel mantello, ad es. lungo archi di isole (trench).
~t1/2