Metodi Matematici per l`Ingegneria

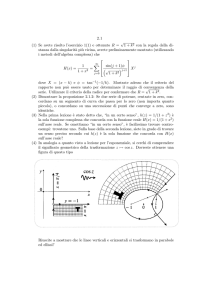
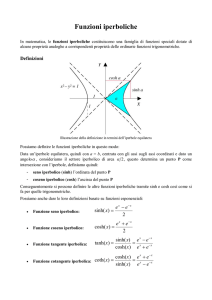
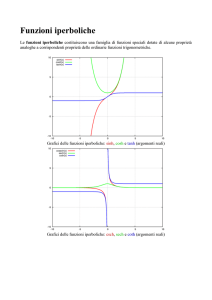
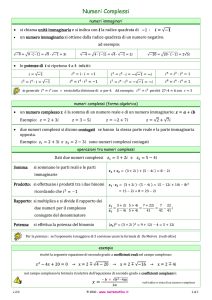
Metodi Matematici per l’Ingegneria
Davide Buoso
Esercitazione del 08/03/2016
Un po’ di teoria
Cominciamo ricordando che un numero complesso z può essere scritto in due
modi:
• in forma algebrica, con parte reale e parte immaginaria:
z = x + iy,
ove x e y sono numeri reali. Nel piano di Gauss, la parte reale x rappresenta l’ascissa, mentre la parte immaginaria y rappresenta l’ordinata;
• in forma trigonometrica, con modulo e argomento:
z = ρ(cos θ + i sin θ),
ove ρ è reale positivo e θ è un numero reale. Nel piano di Gauss, il modulo
rappresenta la distanza tra z e l’origine (che altri non è che il numero 0),
mentre θ rappresenta l’angolo tra l’asse reale e il vettore da 0 a z; ciò è
del tutto analogo alle coordinate polari in R2 .
Introduciamo a questo punto la formula di Eulero:
ea+ib = ea (cos b + i sin b).
Osserviamo subito due cose molto importanti:
• se z = ea+ib , allora il modulo di z è ea e il suo argomento è b;
• abbiamo una definizione delle funzioni trigonometriche in termini dell’esponenziale complesso.
Più in generale, possiamo definire le funzioni trigonometriche in C in modo
seguente
eiz − e−iz
eiz + e−iz
, sin z =
.
cos z =
2
2i
È chiaro che le funzioni cosı̀ definite sono una generalizzazione delle funzioni
trigonometriche classiche definite sui reali.
Definiamo qui anche le funzioni iperboliche
cosh z =
ez + e−z
ez − e−z
, sinh z =
.
2
2
1
Queste funzioni come si vede sono molto simili alle loro cugine trigonometriche.
Mentre queste ultime servono a parametrizzare circonferenze ed ellissi, le funzioni iperboliche si possono usare per parametrizzare le iperboli. Di più, cosh
è pari (come cos) e sinh è dispari (come sin). Inoltre, soddisfano l’uguaglianza
fondamentale
(cosh z)2 − (sinh z)2 = 1 ∀z ∈ C.
Come funzioni di variabile reale, non sono periodiche a differenza delle funzioni
trigonometriche. Notiamo però che cosh x è sempre maggiore o uguale a 1 (con
uguaglianza solo per x = 0) e il suo grafico assomiglia ad una parabola con
vertice in (0, 1) (ma attenzione! non è una parabola), invece sinh x ha lo stesso
segno di x (e sinh 0 = 0), e il suo grafico assomiglia ad una cubica.
Osserviamo anche che, analogamente alle funzioni trigonometriche, si possono introdurre anche i corrispettivi iperbolici di tangente, cotangente, secante
e cosecante.
Concludiamo con le seguenti identità che legano funzioni trigonometriche e
funzioni iperboliche:
cosh iz = cos z, cos iz = cosh iz,
sinh iz = i sin iz, sin iz = i sinh iz.
Esercizi
Esercizio 1. Scrivere i seguenti numeri complessi in forma trigonometrica:
z = 2 + 2i, z = −5 + 3i.
Svolgimento. √Cominciamo con z = 2 + 2i. Anzitutto osserviamo che |z| =
√
22 + 22 = 2 2. Ricordando che l’argomento di un numero complesso è l’arcotangente del rapporto tra la sua parte
√ immaginaria e quella reale, abbiamo
allora θ = arctan 1 = π/4. Quindi z = 2 2(cos π4 + i sin π4 ).
Il resto è lasciato come esercizio per casa.
5
Esercizio 2. Scrivere i seguenti numeri complessi in forma algebrica: z = 3e 6 πi ,
√ π
z = 2e 3 i .
5
Svolgimento. Cominciamo con z = 3e 6 π . Abbiamo
√
√
5
5
3
i
3 3 3
z = 3(cos π + i sin π) = 3(−
+ )=−
+ i.
6
6
2
2
2
2
Il resto è lasciato come esercizio per casa.
Esercizio 3. Risolvere l’equazione iz 2 − 2z̄ − 2 − i = 0.
Svolgimento. Poniamo z = x + iy, con x, y ∈ R. L’equazione diventa
i(x2 − y 2 + 2ixy) − 2x + 2iy − 2 − i = 0,
da cui
(−2xy − 2x − 2) + i(x2 − y 2 + 2y − 1) = 0.
2
Ricordiamo che un numero complesso è uguale a zero se e solo se parte reale e
parte immaginaria sono ambedue nulle. Quindi
xy + x + 1 = 0,
x2 − y 2 + 2y − 1 = 0,
e risolvendo la seconda equazione per y otteniamo
y = 1 ± x.
Ora andiamo a sostituire nella prima equazione.
• Se y = 1 + x, allora
x(1 + x) + x + 1 = 0,
da cui otteniamo (x + 1)2 = 0, quindi x = −1.
• Se y = 1 − x, allora
x(1 − x) + x + 1 = 0,
√
da cui otteniamo x − 2x − 1 = 0, quindi x = 1 ± 2.
√
√
√
√
Quindi le soluzioni sono z = −1, z = 1 + 2 − i 2, z = 1 − 2 + i 2.
2
Esercizio 4. Risolvere l’equazione z̄ 3 + z 2 = 0.
Svolgimento. Abbiamo z̄ 3 = −z 2 , da cui
|z|3 = |z|2 ,
ovvero z = 0 oppure |z| = 1. Ora, se z 6= 0 abbiamo
z̄ 5 = −z 2 z̄ 2 = −|z|4 = −1,
quindi
z 5 = −1.
Ricordiamo che −1 = eπi , quindi le soluzioni sono
z=e
2k+1
5 πi
, per k = 0, . . . , 4.
Esercizio 5. Risolvere l’equazione sin z = i.
Svolgimento. Ricordiamo che sin z =
eiz −e−iz
.
2i
Quindi l’equazione diventa
eiz − e−iz
= i,
2i
da cui otteniamo e2iz + 2eiz − 1 = 0, ovvero
√
eiz = −1 ± 2.
Ora poniamo z = x + iy e scriviamo
e−y (cos x + i sin x) = −1 ±
3
√
2.
Siccome il membro di destra ha parte immaginaria nulla, deduciamo che pure
il membro di sinistra deve avere tale proprietà e quindi x = kπ per k intero.
Arriviamo quindi a
√
√
e−y = (−1)k ± 2 = ±1 ± 2.
Siccome il membro di sinistra è√sempre positivo, gli unici valori accettabili√per
il membro di destra sono ±1 + 2, da cui otteniamo che y = − ln((−1)k + 2),
quindi
√
z = kπ − i ln((−1)k + 2), k ∈ Z.
Esercizio 6. Risolvere le seguenti equazioni: z 2 −(2+3i)z+3i = 0, iz 2 +z 2 z̄ = 0,
cos z = 2, 2 cosh z + sinh z = 1.
Svolgimento. Esercizio per casa.
4