1. PROBABILITA`. CONCETTI FONDAMENTALI Gli eventi reali

1. PROBABILITA'. CONCETTI FONDAMENTALI
Gli eventi reali possono essere generalmente associati ad una di due
categorie principali:
-
eventi che possono essere replicati (con ciò implicando condizioni
ripetitive, identiche),
eventi considerati unici, o rari (nella scala dei tempi considerata).
Come esempio della prima categoria di eventi possiamo menzionare l'uscita
di un numero alla roulette, o il guasto di un componente meccanico durante
delle prove in condizioni controllate, riproducibili.
Come esempio della seconda categoria di eventi possiamo menzionare la
posizione che avrà all'arrivo un dato cavallo in una corsa, o il guasto di un
sistema meccanico durante la sua missione (per es., la rottura del cambio di
un'auto durante una corsa), o l'eventualità di un terremoto in una data
regione in un intervallo di tempo determinato.
Se la probabilità di un dato evento è una quantità con cui misurare il grado
di fiducia, o confidenza, sulla sua riuscita, basandoci sulle nostre
conoscenze in un determinato momento, due definizioni distinte di essa
potranno quindi essere formulate, a seconda dell'appartenenza all'una od
all'altra delle categorie sopra citate.
Così, in rapporto agli eventi della prima categoria, avremo la definizione
"frequentista" per la quale, dato un evento X, la probabilità, P(X), del suo
avverarsi in una certa prova è data dal rapporto tre il numero di eventi
favorevoli (cioè corrispondenti all'evento X) ed il numero di tutti gli eventi
possibili, assumendo condizioni identiche in ciascuna prova (come
succede, ad esempio, con le giocate alla roulette).
Per quanto riguarda invece la seconda categoria di eventi, avremo la
definizione "soggettivista" secondo la quale, dato un evento X, la
probabilità, P(X), del suo avverarsi in una certa prova corrisponde ad una
valutazione quantitativa personale (e quindi soggettiva) del suo avverarsi
(come la posizione in classifica di un cavallo alle corse su cui
scommettiamo). Si suppone che questa valutazione soddisfi comunque i
criteri di autoconsistenza e compatibilità con le altre informazioni
disponibili.
1.2. Probabilità di eventi
Eventi congiunti
Il risultato congiunto, o intersezione, di due generici eventi X e Y è
indicato con la notazione X I Y (X AND Y). La probabilità di questa
intersezione, P ( X I Y ) , è normalmente denotata P(XY). Introducendo il
concetto di probabilità condizionata P(X|Y), cioè, la probabilità dell'evento
X dato Y, si può scrivere la relazione
P ( X I Y ) ≡ P ( XY ) = PX | U ) P (Y )
(1.1)
L'estensione ad eventi multipli è immediata. Per esempio, nel caso di tre
eventi X, Y e Z, si ha
P ( X I Y I Z) ≡ P ( XYZ ) = P ( X | YZ )P ( Y | Z) P( Z ) .
(1.2)
Se, oltre ad X, introduciamo il suo complemento X (NOT X), cioè l'evento
che X non abbia luogo, questi due eventi si escludono a vicenda e la
probabilità di verificarsi contemporaneamente si annulla, cioè
P( XX) = P( X | X )P( X) = 0 .
(1.3)
Eventi disgiunti
Consideriamo ora il risultato di due eventi disgiunti X e Y. Chiameremo
questo evento l'unione di X ed Y e lo denoteremo con XU Y (X OR Y). La
probabilità di questa unione, P(XU Y), è normalmente denotata P(X+Y). Si
può scrivere la seguente espressione:
P(X+Y) = P(X) + P(Y) − P(XY) ,
(1.4)
dove P(XY) corrisponde alla alla probabilità dell'evento congiunto
(intersezione) di X e Y. Anche in questo caso l'estensione ad eventi multipli
è immediata. Per esempio, nel caso di tre eventi X, Y e Z, risulta
P(XU Y U Z) ≡ P(X+Y+Z)
= P(X) + P(Y) + P(Z) − P(XY) − P(XZ) − P(YZ) + P(XYZ)
(1.5)
In relazione agli eventi X e X (NOT X) la probabilità del loro risultato
disgiunto è
P( X + X) = P( X) + P( X ) = 1 .
(1.3)
2. VALUTAZIONE PROBABILISTICA DEI COMPONENTI
Un sistema è una struttura formata da uno o più componenti, od unità, o
elementi (generalmente soggetti a riparazione, in caso di guasto). Qui ci
limiteremo a considerare tali componenti. I concetti principali che si
otterranno, come quelli relativi alla affidabilità o alla disponibilità, possono
essere tuttavia anche estesi ad interi sistemi (o sottosistemi).
Distingueremo dapprima tra due tipi di componenti: quelli che operano su
richiesta e quelli che operano di continuo.
Componenti che operano su richiesta
Per quanto riguarda i componenti che operano su richiesta, potremo
definire la probabilità che all' l -esima richiesta il componente sia in
operazione (evento X l ). La probabilità che il componente sia in operazione
a ciascuna di L richieste sarà data dall'equazione
P(X1X2 ... XL) = P(XL| X1 X2 ... XL-1) P(X1 X2 ... XL-1)
≡ P(XL| X1 X2 ... XL-1) P(XL-1| X1 X2 ... XL-2) ... P(X2|X1)P(X1)
(1.4)
Componenti che operano di continuo
Per quanto riguarda i componenti che operano di continuo, indichiamo con
F(t) la probabilità (cumulativa) che il tempo del loro primo guasto sia
inferiore od eguale al tempo t di continua operazione. Ovviamente, è
0 ≤ F( t ) ≤ 1. La corrispondente funzione di distribuzione delle probabilità
(p.d.f.) f(t) sarà data dall'equazione
f (t) =
dF( t )
dt
( t > 0)
(1.5)
La quantità f(t)dt corrisponde alla probabilità che il primo guasto avvenga
tra t e t+dt.
Introduciamo ora il tempo medio alla rottura (MTTF, per "mean time to
failure"), cioè il tempo medio che il componente ha funzionato prima della
rottura. Esso sarà dato dall'espressione
∞
MTTF =
∫ tf (t)dt
.
(1.6)
o
Affidabilità dei componenti
La probabilità che nell'intervallo (0,t) non avvengano guasti, nel senso che
durante questo tempo il componenti operi normalmente, è chiamata
"affidabilità" (ingl.: reliability) ed è denotata con R(t). Otteniamo
facilmente
R(t) = 1 − F( t ) =
∞
∫ f (t)dt
.
(1.7)
t
Chiaramente, R ( t ) → 0 per t → ∞ . Dall'espressione (1.7) vediamo che F(t)
corrisponde al complemento dell'affidabilità, cioè a [1 − F( t )] . Questa
quantità è chiamata "inaffidabilità" (ingl.: unreliability) ed è denotata
R (t) .
Poiché è
dR( t )
= − f (t ) ,
dt
(1.8)
dalla (1.6) otteniamo che il tempo medio al guasto è dato dall'espressione
∞
MTTF =
∫ R (t)dt
.
(1.9)
o
La funzione di distribuzione della probabilità di primo guasto f(t) relativa
ad un componente è normalmente espressa dal prodotto
f(t) = λ(t)R(t) ,
(1.10)
dove λ(t) viene definito il tasso di guasto istantaneo, generalmente
conosciuto come "tasso di rischio" (ingl.: hazard rate). La quantità f(t)dt ha
il significato di una probabilità condizionata. Infatti, essa corrisponde alla
probabilità che tale componente sia soggetto a guasto nel tempo dt dopo
aver funzionato normalmente fino al tempo t.
Poiché è f ( t ) = −
λ(t) =
dR( t )
, si ha
dt
f (t)
1 dR( t )
= −
R( t )
R ( t ) dt
(1.11)
e quindi le relazioni
R(t) = e
− ∫ t λ ( t) dt
o
f(t) = λ(t) e
t
o
− ∫ λ ( t) dt
(1.12)
.
(1.13)
L'equazione (1.12) è chiamata l'equazione fondamentale dell'affidabilità,
data la sua importanza nei casi pratici. Infatti, l'informazione dei dati
statistici sull'affidabilità dei componenti è generalmente data attraverso i
valori di λ(t).
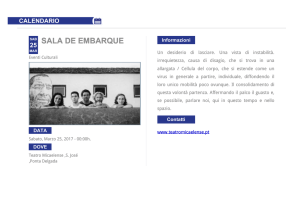
Il comportamento nel tempo di λ(t) segue generalmente la cosiddetta
"curva a vasca da bagno" (bath tub curve) (v. figura 1), caratterizzata cioè
da tre periodi: un primo periodo con λ(t) all'inizio relativamente grande e
quindi decrescente esponenzialmente per la progressiva eliminazione di
tutte le unità difettose; un secondo periodo, più o meno lungo, con λ(t)
relativamente costante, chiamato periodo di vita utile; un terzo periodo,
chiamato periodo di invecchiamento, durante il quale λ(t) aumenta
rapidamente con il tempo a seguito di processi di degradazione. In pratica, i
componenti sono usati solo durante il periodo di vita utile, cioè dopo prove
iniziali e prima dell'inizio dei processi di degradazione. Poichè in questo
periodo il valore λ può essere considerato costante, l'espressione
dell'affidabilità può essere semplificata e risulta
R(t) = e
−λt
.
(1.14)
Corrispondentemente, anche l'espressione del tempo medio al guasto
(MTTF) si semplifica. Ricordando la (1.9), si può scrivere
∞
MTTF =
∫ R (t)dt
o
= 1/λ .
(1.15)
λ(t)
t
Fig. 1. Curva a vasca da bagno λ(t)
Disponibilità dei componenti
L'affidabilità R(t) di un componente dà la probabilità che esso non abbia
subito eventi di guasto fino al tempo t e si applica sia ad elementi non
riparabili che ad elementi riparabili. Introduciamo ora il concetto di
"disponibilità" (ingl.: availability) che si applica ad un componente che,
essendo riparabile, può tollerare condizioni di stato di guasto. In questi casi
la disponibilità corrisponde alla probabilità che tale componente sia in
operazione ad un dato istante t e viene denotato come A(t). Il suo
complemento, A( t ) = 1 − A( t ) viene chiamato "indisponibilità" (ingl.:
unavailability). Ovviamente è R ( t ) ≤ A( t ) ≤ 1, dove l'equazione
R ( t ) = A( t ) vale per componenti non riparabili.
Consideriamo il caso di un sistema formato da un singolo componente e
definiamo il tasso µ(t) di riparazione istantaneo, così come λ(t) è stato
definito come tasso di guasto istantaneo, o tasso di rischio). Se il tasso di
riparazione istantaneo è costante, ciò significa assumere che i tempi di
riparazione (da non confondersi con i tempi in cui inizia la riparazione)
sono distribuiti in modo casuale (ingl.: random). Abbiamo già visto come
in rapporto al valore costante λ il tempo medio al guasto MTTF è dato da
1/ λ. In modo del tutto analogo, in rapporto al valore costante µ, il tempo
medio alla riparazione MTTR (solitamente << MTTR ) è dato da 1/µ . La
somma MTTF+MTTR corrisponde al tempo medio tra due guasti (MTBF,
per l'ingl.: mean time between failures). Avendo assunto processi di
riparazione casuali con un tasso istantaneo µ, si trova facilmente che la
distribuzione dei tempi di riparazione segue una legge esponenziale, cioè
µ exp[−µ( t − t )] , dove t rappresenta il tempo del guasto a partire dal quale
la riparazione ha luogo.
A tempi asintotici, con valori costanti di l e µ, la disponibilità è data dal
rapporto tra MTTF (=1/λ) e MTBF (= 1/λ + 1/µ), cioè
A( ∞ ) =
1/ λ
µ
=
.
1/ λ + 1/ µ λ + µ
(1.16)
2. DISTRIBUZIONI STATISTICHE E STIME DI PARAMETRI
Descriveremo brevemente nel seguito alcune distribuzioni statistiche di
interesse in relazione agli eventi di guasto di componenti ed alcuni criteri
con cui i parametri che definiscono queste distribuzioni possono essere
valutati a partire da dati statistici.
2.1 Distribuzioni statistiche
Distribuzione binomiale
Questa distribuzione viene usata per elementi caratterizzati da due possibili
stati [evento X/evento X (NOT X), o UP/DOWN, o successo/insuccesso]
in cui il numero totale di prove (L) è conosciuto. Per esempio, si può
applicare ai componenti operanti a richiesta.
Si parte dall'evidente equazione
[ P( X) + P( X )] = 1 .
L
(2.1)
Il generico termine a sinistra risulta
L!
P( X ) n P( X) L − n
P(n) =  L  P( X) n P( X) L − n ≡
n
 
n! ( L − n)!
(2.2)
e rappresenta la probabilità che in n (di un totale di L) prove il risultato sia
un insuccesso (evento X ).
Valore medio di n:
n=
L
∑ nP(n) = LP(X )
.
(2.3)
n =0
Varianza di n:
σ =
2
L
∑ ( n − n)
2
P(n ) = LP( X) P( X) .
(2.4)
n =0
Probabilità cumulativa, su L prove, di numero di evento di guasto ≤ x :
x
P( n ≤ x) =
∑ P( n)
.
(2.5)
n =0
Distribuzione di Poisson
Si ottiene dalla distribuzione binomiale relativa ad un numero molto grande
di prove identiche per ciascuna delle quali la probabilità di insuccesso
P( X ) è molto piccola. Per L → ∞ e P( X ) → 0 si ottiene facilmente
−µ
e µ
P( n) =
n!
n
,
(2.6)
dove µ qui rappresenta il numero medio di insuccessi (risulta anche eguale
alla varianza)
Distribuzione Erlanghiana
E' la distribuzione continua ottenuta da quella di Poisson ponendo il
numero complessivo degli insuccessi µ=λt, avendo assunto λ costante.
Risulta
P( n, t ) =
e
− λt
n!
( λt ) n .
(2.7)
Probabilità che l'n'esimo guasto avvenga in tra t e t+dt, essendosi già
verificati (n-1) guasti:
λ( λt ) n −1 e − λ t dt
f n ( t )dt = λP( n − 1, t )dt =
( n − 1)!
(2.8)
Ponendo n=1 si ottiene la distribuzione di primo guasto. Scrivendo f(t) in
luogo di f1(t) si ha:
f(t) = λe
−λt
che coincide con la distribuzione esponenziale.
(2.9)
Distribuzione gamma
E' una distribuzione usata per rappresentare situazioni in cui il componente
considerato è soggetto ad eventi ripetitivi, come shock termici, fenomeni di
fatica, ecc. In questo caso la probabilità di guasto dipende dal numero di
eventi verificatisi. Essa è data dall'espressione
λ( λt ) n −1 e − λt dt
f (t) =
Γ( n)
(λ>0; n>0)
(2.10)
dove n può anche non essere un intero. Se n è intero, essendo in questo
caso Γ(n ) ≡ n! , si ottiene di nuovo la distribuzione Erlangiana.
Distribuzione lognormale
Si consideri la distribuzione normale (Gaussiana) di una quantità t:
y(t) =
2
2
1
− ( t − t ) / 2σ
e
2π σ
(2.11)
dove t e σ2 sono il valore medio e la varianza di x, rispettivamente.
Poniamo ora nella (2.10) lnt , il suo valore medio (espresso come lnβ) e la
sua varianza α 2 in luogo di t, t e σ2, rispettivamente. Si otterrà la cosiddetta
distribuzione lognormale:
f(x) =
2
2
1
−[ln( t / β)] / 2 α
e
2 π αt
(2.12)
dove la presenza del coeficiente 1/t nel membro a destra dipende dal fatto
che si è mantenuto l'argomento t, piuttosto che lnt , cioè la distribuzione è
stata moltiplicata per
dln t 1
≡ .
dt
t
Valore medio di t:
t = βe −α
Varianza di t:
2
/2
(2.13)
σ 2 = β 2 e −α
2
2
(exp α −1)
.
(2.14)
La distribuzione lognormale ha rilevanza per quantità che si assume avere
sempre valori positivi
Distribuzione di Weibull
.Questa distribuzione è usata per descrivere ognuno dei tre periodo definiti
in relazione alla curva a "vasca da bagno" incontrata precedentemente. Essa
si presenta nella forma:
f(t) = λ( t )e
−λ (t )t / β
(2.15)
dove λ = αβ t β −1 ed α è un parametro di scala.
Se β<1, la funzione λ(t) presenta un andamento decrescente (periodo
iniziale).
Se β=1, allora λ=α e si ha la distribuzione esponenziale (periodo utile).
Se β>1 la funzione λ(t) presenta un andamento crescente (andamento finale
di invecchiamento).
2.2 Stima dei parametri
Dati i tempi di guasto ottenuti sperimentalmente relativi ad un campione di
J componenti identici ( o da J misure rrelative allo stesso componente), si
pone di determinare la distribuzione del tempo di guasto per componenti di
questo tipo. Descriveremo nel seguitotre metodi largamente usati a questo
scopo: il metodo dei momenti, il metodo della massima verosimiglianza, il
metodo della massima entropia.
Metodo dei momenti
Dati i tempi di guasto ottenuti da J componenti, il metodo dei momenti
consiste nel valutare dapprima il loro valore medio e la varianza , usando le
espressioni
1 J
∑tj
J j=1
t =
σ2 =
(2.16)
1 J
(t j − t) 2
∑
J − 1 j=1
(2.17)
dove tj rappresenta il tempo di guasto del componente j'esimo. Una volta
che t e σ2 sono dati, assieme alla curva di distribuzione appropriata
(esponenziale, gamma, ecc.), i parametri che la caratterizzano
(normalmente non eccedenti il numero di due, come abbiamo visto nei
paragrafi precedenti) possono quindi essere stimati attraverso le relazioni
che li legano al valor medio ed alla varianza.
Metodo della massima verosimiglianza
Il metodo della massima verosimiglianza (ingl.: maximum likelihood
method) consiste nel determinare quei parametri che massimizzano la
funzione di verosimiglianza
L( t 1 , t 2 ,..., t J | θ1 , θ 2 ,..., θ M ) =
J
∏ f (t j | θ1 , θ 2 ,..., θ M )
(2.18)
j=1
dove θ1 , θ 2 ,..., θ M rappresentano i parametri i cui valori si vogliono
stimare, mentre
f ( t j | θ1 , θ 2 ,..., θ M ) rappresenta la funzione di
~
distribuzione scelta per i tempi di guasto misurati tj. Poiché i valori θm che
massimizzano la funzione L sono gli stessi che massimizzano il suo
logaritmo, per determinarli è preferibile considerare la quantità lnL. Questo
significa porre
∂ ln L
= 0
∂θ m
(m=1,2,...,M)
(2.19)
~
La soluzione di questa equazione consente di ottenere le stime θm . Inoltre,
la stima della loro varianza risulta
~
σ 2m
 ∂ 2 ln L 

= −
 ∂θ 2 

m 
−1
(m=1,2,...,M)
(2.20)
Metodo della massima entropia
L'idea di usare la teoria dell'informazione per predire la distribuzione di un
insieme di eventi elementari distribuiti in forma random ha origine dalla
considerazione che questi, per il fatto stesso di essere random, tendono a
presentarsi nel maggiore disordine possibile (entro i vincoli assegnati),
sicché la conoscenza relativa ad uno qualsiasi di essi risulta essere
massimamente "informativa". 1 Pertanto, lo loro distribuzione può essere
ottenuta massimizzando questa "informatività". Per esprimerla
numericamente si è fatto ricorso al concetto di entropia utilizzato per la
distribuzione delle velocità di un gas contenuto in un recipiente ad una
temperatura fissata. Come noto, in questo caso le velocità delle molecole
del gas si distribuiscono in modo tale che il numero di microstati, o
configurazioni nello spazio delle fasi, in condizioni di equilibrio
termodinamico, sia massimo, il che corrisponde alle condizioni di massimo
disordine del gas stesso. In rapporto a questo, si può dire che in questo caso
la conoscenza delle coordinate spaziali ed energetiche di una molecola è
massimamente "informativa". L'entropia del sistema è definita come
S=ln kW, dove k è la costante di Boltzmann e W il numero di
configurazioni possibili. Sfruttando questa analogia, è stata definita
l'entropia dell'informazione, data dall'espressione
SI = −
1
∑ Pi ln Pi ,
ln 2 i
(2.21)
dove la somma è estesa a tutti i possibili eventi e dove Pi rappresenta la
probabilità che accada l'evento i'esimo. Essa va intesa come probabilità
condizionata, cioè Pi = P(Xi|Y), dove Y rappresenta l'informazione a priori
assegnata (stime di dati, vincoli, ecc.). La funzione SI può essere vista come
la misura dell'informazione mancante, corrispondente al numero di
domande (in termini di bits, cioè si/no, o vero/falso) che sarebbero
necessarie per identificare con certezza l'occorrenza di un evento (per es., il
risultato di una misura) 2. Dato un numero di possibili eventi, si può
dimostrare che l'entropia SI risulta massima se essi sono ugualmente
distribuiti. Dell'informazione teorica o sperimentale che escluda alcune
possibilità naturalmente la ridurrebbero.
1
Se consideriamo il caso limite opposto, di un insieme di eventi non random, cioè predeterminati, l'informazione
contenuta dalla rilevazione (in questo caso, verifica) di uno di essi sarebbe ovviamente nulla, il loro accadere essendo
conosciuto in partenza.
2
Per esemplificare, consideriamo un sistema formato da un solo componente, soggetto ad una probabilità di guasto π.
1
1
L'entropia del sistema sarà S I = −
∑ Pi ln P i ≡ −
∑ P i ln P i
ln 2 i
ln 2 i
Consideriamo ora il caso di J componenti identiche (il che implica una
comune funzione di distribuzione dei guasti) soggette a test. I tempi di
guasto risultano tj (j=1,2,...,J), da cui possono essere ricavati stime dei
valori medi e delle varianze.
Se suddividiamo il tempo in intervalli uguali dt r = ( t r +1 − t r ) , avendo
posto to=0, e definiamo con Pr la probabilità che il componente in esame si
guasti nell'intervallo dt r , allora l'equazione (2.21) può essere scritta , a
parte un coefficiente costante,
∞
S I = −∑ Pr ln Pr .
(2.22)
r =1
Assumendo l'ovvio vincolo
∞
∑ Pr
= 1
(2.23)
r =1
ed altri del tipo
∞
∑ Tm (t r )Pr
r =1
= Tm ,
(m=1,2,...,M)
(2.24)
dove T m e Tm rappresentano M funzioni date il loro valore medio (di cui si
conoscono delle stime), rispettivamente, la funzione da massimizzare, che
chiameremo F, risulterà
∞
∞
∞
r =1
r =1
F = − ∑ Pr ln Pr + ( k o − 1)( ∑ Pr − 1) + k1 ( ∑ T1 ( t r ) Pr − T1 )
r =1
∞
+ ... + k M ( ∑ TM ( t r ) Pr − TM )
(2.25)
r =1
dove (ko-1), k1,...,kM sono i moltiplicatori di Lagrange.
Differenziando rispetto a Pr, si ottengono le equazioni
dF
dPr
= − ln Pr + k o + k 1T1 ( t r ) + ... + k M TM ( t r ) = 0
(r=1,2,...)
(2.26)
da cui si ottiene
Pr = e
− k o − k1T1 ( t r ) − ...− k M TM ( t r )
(r=1,2,...)
(2.27)
da cui i valori dei moltiplicatori di Lagrange ko, k1,...,kM si possono ottenere
usando i vincoli (2.23) e (2.24).
Se in luogo delle probabilità discrete Pr poniamo f r δt r , dove f r è il valore
medio della densità di probabilità del guasto del componente nell'intervallo
δt r , e facciamo quindi tendere δt r a zero, otteniamo la densità (continua)
di distribuzione
f (t r ) =
lim f r = e − k o − k1T1( t r ) −... − k M TM ( t r ) .
δt r →0
(tr ≥ 0)
(2.28)
Come detto sopra, i valori dei moltiplicatori di Lagrange ko, k1,...,kM
possono essere ottenuti usando i vincoli, che in questo caso
corrisponderanno alle equazioni (2.23) e (2.24), con lasomma sostituita dal
corrispondente segno di integrale. Possiamo quindi scrivere
∞
∫ f (t)dt
= e
o
∞
∫ Tm (t )f (t)dt
o
−k o
∞
∫e
− k 1T1 ( t r ) −... − k M TM ( t r )
dt = 1
(2.29)
o
= e
−k o
∞
∫ Tm (t)e
− k1T1 ( t r ) − ... − k M TM ( t r )
dt = Tm
o
(m=1,2,...,M)
(2.30)
Da queste equazioni si ricava facilmente
∞
dk o
dk o
d[exp(−k o ]
=
Tm = − ∫ Tm f ( t )dt = −Tm .
dk m
d[exp(−k o ]
dk m
o
(m=1,2,...,M)
(2.31)
Ora si danno due possibilità, a seconda se la funzione di distribuzione
specifica relativa agli eventi considerati e sconosciuta, o il tipo cui essa
appartiene è noto e desideriamo determinare i parametri che la definiscono.
Nel primo caso, l'informazione rappresentata dalle quantità Tm
_
(generalmente i momenti t n ) consentiranno di determinare i valori ko,
k1,...,kM (e quindi la legge di distribuzione). Nel secondo caso, è necessario
esprimere la funzione data nella forma data dalla (2.28) e quindi, usando la
(2.31), determinare i suoi parametri.
A titolo di illustrazione, consideriamo una quantità di cui conosciamo solo
la stima del suo valore medio. Assumiamo che questo valore sia il tempo
medioal guasto (MTTF=t ) di un componente. In questo caso M=1 e
possiamo usare solo due vincoli. I corrispondenti moltiplicatori di
Lagrange possono essere ottenuti dalle due equazioni
e
−k o
∞
∫e
− k 1t
dt =
o
e
−k o
∞
∫ te
− k 1t
dt =
o
e
−k o
k1
e −k o
k12
= 1
=
(2.32)
1
k1
= t .
(2.33)
Risulta quindi k 1 = 1 / k e k o = − ln(1 / t ) . La funzione di distribuzione
sarà quindi, ponendo λ in luogo di 1 / t ,
f ( t ) = λe − λ t
(2.34)
cioè troviamo che la distribuzione esponenziale è quella più probabile in
assenza di informazione supplementare.
E' anche immediato verificare che , se avessimo scelto a priori la
distribuzione esponenziale come quella adatta agli eventi considerati,
avremmo trovato che λ =1 / t .
Se, oltre alla stima del valore medio t , avessimo avuto anche la stima della
varianza, ma nessuna informazione sui momenti di ordine superiore e
neppure sul tipo di curva si debba applicare, avremmo ottenuto la ben nota
distribuzione normale Gaussiana. Se, oltre al primo e secondo momento,
avessimo avuto ragione di credere che la distribuzione esponenziale è
quella più appropriata, sulla base di una valutazione personale fondata
sull'esperienza e su casi simili precedenti, l'informazione relativa alla
varianza non dovrebbe essere considerata. Infatti, con la distribuzione
esponenziale, come abbiamo visto nei paragrafi precedenti, la varianza è
2
data dal quadrato del valore medio (in questo caso da t ). In questo caso,
l'informazione sulla varianza potrebbe essere semmai usata per verificare la
validità della scelta della distribuzione esponenziale.