Dinamica di reti neurali diluite con accoppiamento impulsivo

annuncio pubblicitario

ANNO ACCADEMICO 2008-2009
Facoltà di Scienze Matematiche, Fisiche e Naturali
Corso di Laurea in Fisica
Tesi di Laurea
Dinamica di reti neurali diluite
con accoppiamento impulsivo
Candidata:
Simona Olmi
Relatore:
Correlatore:
prof. Roberto Livi
dott. Alessandro Torcini
25 giugno 2009
Indice
Introduzione
1
1 Elementi di neurofisiologia
5
1.1 I neuroni . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
1.2 I segnali neuronali ed il potenziale di azione . . . . . . . . . . . . . .
7
1.3 Le sinapsi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1.4 Introduzione alla dinamica neuronale . . . . . . . . . . . . . . . . . . 11
1.5 La membrana cellulare del neurone . . . . . . . . . . . . . . . . . . . 13
1.6 Canali ionici e correnti ioniche . . . . . . . . . . . . . . . . . . . . . . 15
1.7 Origine del potenziale di riposo . . . . . . . . . . . . . . . . . . . . . 17
1.7.1
Un modello cellulare semplificato . . . . . . . . . . . . . . . . 17
1.7.2
L’equazione di Nerst . . . . . . . . . . . . . . . . . . . . . . . 19
1.7.3
Effetto del sodio e pompe ioniche . . . . . . . . . . . . . . . . 20
1.7.4
Effetto della permeabilità ionica e dei meccanismi di trasporto 21
1.8 Proprietà elettriche passive della membrana . . . . . . . . . . . . . . 23
2 Modelli semplificati di neuroni
26
2.1 Dal modello di Hodgkin-Huxley al modello leaky integrate-and-fire . . 28
2.2 Neuroni leaky integrate-and-fire . . . . . . . . . . . . . . . . . . . . . 33
2.2.1
Correnti sinaptiche . . . . . . . . . . . . . . . . . . . . . . . . 36
I
2.2.2
Adattamento della frequenza di emissione degli impulsi e refrattarietà . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
3 Modelli di reti neurali ad accoppiamento impulsivo
3.1 Reti neurali con accoppiamento impulsivo
41
. . . . . . . . . . . . . . . 42
3.1.1
Modello di rete di neuroni LIF globalmente accoppiati . . . . 44
3.1.2
Mappa guidata dall’evento . . . . . . . . . . . . . . . . . . . . 47
3.1.3
Analisi di stabilità lineare . . . . . . . . . . . . . . . . . . . . 49
3.2 Impulsi di durata finita . . . . . . . . . . . . . . . . . . . . . . . . . . 51
3.2.1
Lunghezze d’onda grandi . . . . . . . . . . . . . . . . . . . . . 53
3.2.2
Lunghezze d’onda brevi
3.2.3
Diagramma di fase e correzioni di taglia finita . . . . . . . . . 54
3.2.4
Altri stati collettivi della rete . . . . . . . . . . . . . . . . . . 57
. . . . . . . . . . . . . . . . . . . . . 54
3.3 Desincronizzazione in reti neurali diluite . . . . . . . . . . . . . . . . 60
4 Dinamica di una rete neurale eccitatoria diluita
66
4.1 Modello della rete in tempo continuo . . . . . . . . . . . . . . . . . . 68
4.1.1
Mappa ad evento guidato . . . . . . . . . . . . . . . . . . . . 69
4.1.2
Algoritmo numerico . . . . . . . . . . . . . . . . . . . . . . . . 71
4.1.3
Scelta aleatoria delle connessioni
. . . . . . . . . . . . . . . . 72
4.2 Analisi di stabilità lineare . . . . . . . . . . . . . . . . . . . . . . . . 74
4.2.1
Reti globalmente accoppiate . . . . . . . . . . . . . . . . . . . 76
4.2.2
Reti diluite . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
4.3 Diagramma di biforcazione . . . . . . . . . . . . . . . . . . . . . . . . 82
4.4 Disordine quenched . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
4.5 Disordine annealed . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
4.6 Confronto con il sistema globalmente accoppiato . . . . . . . . . . . . 100
4.7 Neuroni disaccoppiati guidati dalla rete . . . . . . . . . . . . . . . . . 102
Conclusioni
106
A Fenomenologia delle biforcazioni
109
A.1 Biforcazioni sovra-critiche di punti fissi . . . . . . . . . . . . . . . . . 110
A.2 Biforcazioni sotto-critiche . . . . . . . . . . . . . . . . . . . . . . . . 112
B Metodo della sezione di Poincaré
114
B.1 Mappa di Poincaré . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
B.2 Sezioni di Poincaré per differenti attrattori . . . . . . . . . . . . . . . 116
C Stabilità lineare
120
C.1 Stabilità lineare di orbite periodiche: moltiplicatori di Floquet . . . . 120
C.2 Esponenti di Lyapunov . . . . . . . . . . . . . . . . . . . . . . . . . . 122
C.2.1 Tecnica di calcolo numerico degli esponenti di Lyapunov . . . 126
C.2.2 Dimensione dell’attrattore . . . . . . . . . . . . . . . . . . . . 128
Introduzione
Il presente lavoro di tesi rientra nell’ambito di un’ampia attività di ricerca che ha
visto, negli ultimi anni, un numero crescente di fisici orientarsi verso problematiche
che un tempo erano dominio di biologi, biochimici o fisiologi. In particolare, a
partire dagli studi pionieristici di A.L. Hodgkin e A.F. Huxley sulla fisiologia del
neurone, per i quali ottennero il premio Nobel nel 1963, si è avuto un trasferimento
continuo ed una sempre più vasta applicazione di metodologie propriamente fisiche
al campo delle neuroscienze. Questo ha portato alla realizzazione di analisi sempre
più accurate delle proprietà strutturali e dinamiche sia dei singoli neuroni che di
circuiti neurali presenti in varie aree del cervello.
Scopo di questa tesi di laurea è lo studio dei comportamenti dinamici collettivi
che emergono in reti neurali diluite, in cui i neuroni sono schematizzati con modelli
semplici, ma tali da riprodurre gli aspetti salienti della dinamica neuronale e da
consentire accurate analisi dinamiche e statistiche di reti molto estese. In particolare, intendiamo caratterizzare tali dinamiche collettive identificando gli attratori
corrispondenti e quantificando il loro grado di caoticità.
Prima di riassumere gli aspetti salienti e i risultati contenuti in questa tesi, ci
preme cercare di inquadrarla in una prospettiva più generale, che fa riferimento ad
aspetti di carattere fondamentale. Negli ultimi tre decenni gli studi di reti neurali
si sono intrecciati profondamente a quelli di meccanica statistica sui ferromagneti
aleatori (o vetri di spin) [1], a partire dal modello per memorie associative introdotto
da J.J. Hopfield nel 1982 [2, 3]. Questo modello di rete neurale, oltre ad aver avuto
applicazioni negli ambiti più vari, dalle neuroscienze alla finanza, è stato molto
rilevante anche per gli studi sulla transizione vetrosa, dato che rappresenta uno dei
pochi modelli di vetri di spin risolubili esattamente nel limite termodinamico.
Negli anni più recenti si è passati, anche grazie allo sviluppo di calcolatori più
potenti che ne hanno consentino analisi statisticamente rilevanti, da reti quali quelle
di Hopfield, ove i neuroni sono schematizzati con variabili binarie, a reti in cui la
dinamica del potenziale di membrana di ogni neurone è descritta da variabili di
stato continue, che evolvono secondo una o più equazioni differenziali. Inoltre, stimolati da osservazioni di fisiologia, si è iniziato a considerare reti con accoppiamenti
maggiormente realistici, che vengono realizzati tramite la trasmissione di impulsi.
Queste reti con accoppiamento impulsivo sono state utilizzate ampiamente sia per
studi di neuroscienze computazionali, che per il processamento di immagini e recentemente si è arrivati ad implementare la dinamica di queste reti anche in modo
“hardware”, grazie all’uso di circuiti integrati programmabili [4].
Nello specifico, in questo lavoro di tesi, si sono considerate reti con accoppiamenti eccitatori in cui l’interazione avviene tramite la trasmissione di impulsi di durata
finita. L’interesse per questi modelli è giustificato non solo da analisi teoriche, ma
anche da evidenze sperimentali. In particolare, studi analitici e numerici, svolti
in precedenza per reti globalmente accoppiate, mostrano come in questi sistemi
emergano spontaneamente stati collettivi stabili caratterizzati da dinamiche assolutamente non banali [5, 6]. D’altra parte sono state evidenziate oscillazioni collettive
anche analizzando “in vitro” l’attività elettrica della corteccia cerebrale di topi appena nati, per i quali è noto che le sinapsi sono solo di tipo eccitatorio, dato che le
interazioni inibitorie appaiono solo dopo qualche giorno dalla nascita [7]. Inoltre è
essenziale indagare la robustezza e la stabilità di queste soluzioni collettive rispetto
alla diluizione delle connessioni presenti, visto che nella corteccia cerebrale i neuroni connessi fra loro sono solo una percentuale del totale [8]. Quindi, in questa tesi
indagheremo gli effetti sulla dinamica di stati collettivi oscillatori dovuti al passaggio
da una rete in cui tutti i neuroni sono connessi con tutti, ad una in cui sia presente
una diluizione stocastica nel numero di connessioni afferenti ed efferenti da un determinato neurone. Ci avvarremo quindi di metodologie proprie della meccanica
statistica e dei sistemi dinamici per investigare le proprietà di sincronizzazione e di
auto-organizzazione di un modello non lineare di rete neurale contenente del disordine nella distribuzione delle connessioni, sia congelato (“quenched”) che generato
dinamicamente (“annealed”).
Il primo capitolo della tesi sarà dedicato ad una breve introduzione di semplici
concetti di neurofisiologia, in particolare si riporteranno una schematica descrizione
del neurone, delle sinapsi e della struttura della membrana cellulare. Si descriverà
poi la fenomenologia della dinamica neuronale, con particolare enfasi sulla generazione del potenziale d’azione in termini della dinamica delle correnti ioniche che
attraversano la membrana neuronale.
Nel secondo capitolo saranno introdotti alcuni modelli usati in letteratura per
riprodurre la dinamica dei neuroni, a partire dal modello fisiologicamente rilevante
di Hodgkin-Huxley, per arrivare ad un modello schematico, ma che riproduce gli
elementi fondamentali della dinamica neuronale, quale il modello leaky integrateand-fire [9]. Quest’ultimo modello è assai usato sia nello studio della risposta di
neuroni singoli a stimoli di varia natura, per le possibilità di trattazione analitica
che consente, sia nelle simulazioni di reti complesse con un gran numero di neuroni,
per la semplicità della sua implementazione da un punto di vista numerico.
Il terzo capitolo sarà dedicato ad una rassegna dei risultati più importanti riguardanti le soluzioni collettive osservate in reti con accoppiamenti impulsivi, sia eccitatori
che inibitori. In particolare, per reti globalmente accoppiate eccitatorie si riporterà
un’analisi di stabilità lineare recentemente sviluppata per stati coerenti in reti ove
gli impulsi scambiati hanno durata finita [10]. Per quanto riguarda le reti con accoppiamento inibitorio ricorderemo i risultati di Jin [11] che mostrano come la dinamica
di reti globalmente accoppiate converga sempre su orbite periodiche stabili; inoltre
menzioneremo i risultati di Zillmer et al. [12], che indicano come la diluizione porti
alla nascita di stati transitori stazionari la cui durata cresce esponenzialmente con
il numero di neuroni.
I contributi originali, riportati nel capitolo quarto, riguarderanno lo studio della
dinamica di una rete neurale eccitatoria con accoppiamento impulsivo. Innanzitutto caratterizzeremo in termini di esponenti di Lyapunov le soluzioni collettive
osservate in reti globalmente accoppiate. Questa analisi evidenzierà come, sia lo
stato asincrono che lo stato parzialmente sincronizzato, siano marginalmente stabili
nel limite termodinamico. Descriveremo inoltre come l’introduzione di disordine in
reti finite destabilizzi queste soluzioni rendendole caotiche. Mostreremo poi, come
al crescere del numero di neuroni della rete, la dinamica del campo medio autoconsistente associato a stati parzialmente sincronizzati converga a quella del caso
globalmente accoppiato, sia in presenza di disordine “quenched” che “annealed”.
Nel limite termodinamico mostreremo che il grado di caoticità del sistema dipende
in modo peculiare dal tipo di disordine introdotto nella rete. Infine riporteremo
indicazioni sull’origine del comportamento caotico osservato.
Nelle conclusioni riassumeremo i principali risultati ottenuti in questa tesi ed
esporremo le possibili prospettive e applicazioni future di questi studi. Infine brevi cenni alla teoria delle biforcazioni saranno riportati nell’Appendice A, mentre
l’Appendice B sarà dedicata ad una introduzione della tecnica della sezione di Poincaré. Infine l’Appendice C sarà dedicata ad una sintetica introduzione dell’analisi
di Floquet e degli esponenti di Lyapunov.
Capitolo 1
Elementi di neurofisiologia
I neuroni sono cellule altamente specializzate e si distinguono dalle altre cellule grazie alla loro abilità nel far propagare rapidamente segnali elettrici su lunghe distanze.
Gli impulsi generati dai neuroni, che viaggiano lungo fibre nervose (dette assoni ),
consentono la codifica e la trasmissione di informazione e sono emessi, in seguito a
stimoli esterni, verso altri neuroni. In questo capitolo introdurremo dunque alcuni concetti basilari relativi alla neurofisiologia del neurone, a cominciare dalla sua
morfologia. Caratteristiche morfologiche salienti del neurone sono i dendriti, che
ricevono gli impulsi in ingresso, provenienti da altri neuroni e l’assone, che porta il
segnale in uscita dal neurone verso le altre cellule. Mentre la struttura ramificata del
dendrite permette al neurone di ricevere segnali in ingresso da molti altri neuroni
attraverso le connessioni sinaptiche, l’assone può attraversare lunghe porzioni del
cervello o, in alcuni casi, trasmettere il segnale del singolo neurone attraversando
l’intera spina dorsale. Nei paragrafi successivi daremo una descrizione schematica
del neurone e delle sinapsi; inoltre descriveremo in dettaglio le caratteristiche della
membrana cellulare, sia a riposo che stimolata, con particolare attenzione alle sue
proprietà elettriche. Oltre agli aspetti morfologici analizzeremo anche gli aspetti
fisiologici del neurone ed in particolare tratteremo i meccanismi che sovraintendono
al suo funzionamento e alla generazione dei potenziali di azione in termini della dinamica delle correnti ioniche che attraversano la membrana neuronale. Il potenziale
d’azione è un segnale elettrico in grado di propagarsi per grandi distanze senza attenuazione grazie alle giunzioni mieliniche degli assoni e rappresenta l’unità elementare
di informazione scambiabile tra i neuroni.
1.1
I neuroni
I neuroni sono cellule del sistema nervoso altamente specializzate e dedicate al
trasferimento, immagazzinamento ed elaborazione delle informazioni. Tale elaborazione avviene attraverso segnali elettrici dovuti a differenze di potenziale associate
a correnti elettriche di natura ionica (essenzialmente sono rilevanti solo gli ioni sodio, potassio, calcio e cloro) che attraversano la membrana cellulare del neurone. I
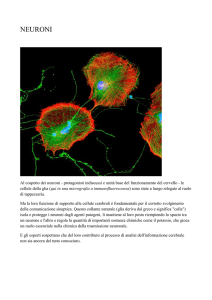
neuroni sono in numero molto elevato e sono connessi fra di loro con topologie assai complesse (vedi figura 1.1): ad esempio nella corteccia cerebrale dei mammiferi
si ha una densità superiore a 104 neuroni/mm3 . Tipicamente, pur nella varietà di
tipi di cellule neuronali (neuroni della corteccia cerebrale, motoneuroni del midollo spinale, ecc.), possiamo riconoscere tre parti morfologicamente e funzionalmente
distinte: il corpo cellulare o soma; i dendriti e gli assoni. Il soma ha una struttura
compatta che risulta approssimativamente sferica (di circa 70 µm di diametro) ed è
sostanzialmente l’unità deputata all’elaborazione dell’informazione. I dendriti sono
estensioni del soma con una struttura molto ramificata che si estendono per distanze
che possono raggiungere il millimetro ed hanno la funzione di raccogliere i segnali
provenienti dagli altri neuroni e trasmetterli al soma. Gli assoni sono lunghe protuberanze (anche oltre un metro nei neuroni motori degli organismi animali superiori)
che si proiettano dal soma e la loro funzione consiste nella trasmissione del segnale
generato dal soma verso i dendriti di un’altro neurone. Usando la terminologia dei
circuiti elettronici si può quindi dire che i dendriti rappresentano il dispositivo di
ingresso (“input”), gli assoni il dispositivo di uscita (“output”) e il soma l’unità
di elaborazione delle informazioni. La morfologia di un particolare tipo di neurone
nonché la sua posizione nella rete neurale forniscono indizi sulla funzione espletata:
ad esempio il livello di arborizzazione fornisce un’idea del numero di connessioni che
può ricevere e verso quante altre cellule neuronali invii i propri segnali (vedi figura
1.2).
Figura 1.1. Neuroni della corteccia dei mammiferi osservati al microscopio. Possiamo distinguere neuroni con corpi cellulari triangolari e circolari: la cellula b è
un classico esempio di cellula piramidale con corpo triangolare [13].
1.2
I segnali neuronali ed il potenziale di azione
Si definisce potenziale di membrana la differenza di potenziale misurata ai capi di
due elettrodi, uno posto all’interno della cellula neuronale ed uno posto nel liquido
extracellulare circostante. Quando si parla di segnale neuronale ci si riferisce alla
variazione temporale e spaziale del potenziale di membrana. Quando il neurone è
a riposo, ossia non è in qualche modo eccitato dall’esterno (e chiariremo nel seguito
cosa si intende), il potenziale di membrana assume un valore caratteristico denominato potenziale di riposo, tipicamente dell’ordine di -65mV, ossia l’interno della
Figura 1.2.
Forme e dimensioni dei neuroni [14].
cellula si trova ad un potenziale inferiore rispetto all’esterno.
I potenziali di azione sono impulsi di tensione tipici, generati durante la dinamica
neuronale; essi hanno una forma pressoché stereotipata e non sono soggetti ad attenuazione o distorsione durante la propagazione lungo l’assone. In figura (1.3) è
riportata la forma tipica di un potenziale di azione. Si notino le seguenti caratteristiche:
• l’impulso di tensione ha una durata di circa 1-2 ms ed una ampiezza misurata
fra il minimo ed il massimo di circa 100-120 mV;
• nella prima fase dell’impulso si assiste ad una crescita veloce del potenziale di
membrana fino ad arrivare ad una fase denominata di depolarizzazione dove
il potenziale di membrana diventa positivo, cioè l’interno della cellula si trova
ad un potenziale superiore rispetto all’esterno;
• nella fase di discesa l’impulso prima di ritornare al valore di riposo passa
attraverso una fase denominata di iperpolarizzazione, tipicamente della durata
di circa 10 ms (e quindi molto più lenta della depolarizzazione), in cui la cellula
presenta un potenziale di membrana inferiore rispetto a quello di riposo.
Il potenziale di azione, che una volta generato nella cellula neuronale, viaggia lungo
l’assone ed è trasmesso agli altri neuroni, costituisce l’unità elementare associata
alla trasmissione dei segnali neuronali. Tipicamente quindi quando ci si riferisce al
segnale emesso da un neurone si intende la sequenza temporale di questi potenziali
di azione, detta anche treno di impulsi (in inglese spike train).
Figura 1.3.
1.3
Forma tipica di un potenziale di azione (o impulso) [15].
Le sinapsi
La sinapsi costituisce essenzialmente la giunzione tra due neuroni ossia la struttura
attraverso la quale le informazioni sono trasferite da una cellula nervosa all’altra. In
tale contesto si definisce neurone presinaptico il neurone “trasmettente” i potenziali
di azione, a monte della sinapsi, e neurone postsinaptico il neurone ’“ricevente” i
potenziali di azione, a valle della sinapsi. Con questa terminologia la sinapsi è quindi la regione in cui l’assone del neurone presinaptico “interagisce” con il dendrite
del neurone postsinaptico. Si definisce inoltre potenziale postsinaptico (che ha come
acronimo PPS ) la risposta in tensione del neurone postsinaptico conseguente all’arrivo del potenziale di azione proveniente dal neurone presinaptico.
Si distinguono essenzialmente due tipi di sinapsi: la sinapsi chimica e la sinapsi
elettrica (altrimenti detta gap-junction). La sinapsi chimica, della quale è riportato lo schema in figura (1.4), risulta la più comune nel cervello dei vertebrati e
si basa sul meccanismo che andiamo a descrivere. Il potenziale di azione generato dal neurone presinaptico, giunto all’estremità dell’assone depolarizza localmente
la membrana cellulare causando il rilascio all’interno della fessura sinaptica (ossia
il piccolo spazio tra le due membrane cellulari presinaptiche e postsinaptiche), da
parte di strutture poste sull’assone denominate vescicole sinaptiche, di particolari
sostanze chimiche denominate neurotrasmettitori. Il neurotrasmettitore, non appena raggiunto il versante postsinaptico della sinapsi, è rivelato da speciali molecole
(chemorecettori ) poste sulla membrana postsinaptica che provocano l’apertura (o
direttamente o tramite una catena di segnali biochimici) di specifici canali attraverso i quali una corrente ionica fluisce dal liquido extracellulare alla cellula. L’ingresso
di questi ioni porta a sua volta ad una variazione del valore del potenziale di membrana postsinaptico. Dunque in una sinapsi chimica si ha prima la trasformazione
di un segnale elettrico in un segnale chimico sulla membrana presinaptica e poi la
successiva trasformazione sulla membrana postsinaptica di un segnale chimico in un
segnale elettrico. La sinapsi elettrica realizza invece un accoppiamento elettrico tra
due neuroni attraverso canali ionici altamente specializzati (detti gap-junctions) che
collegano la membrana presinaptica e postsinaptica. La sinapsi elettrica permette
perciò un flusso di corrente diretto tra neuroni adiacenti ed è quindi più veloce per
la trasmissione del segnale.
Figura 1.4. Esempio di sinapsi chimica: la terminazione presinaptica libera una
sostanza chimica, il neurotrasmettitore, in risposta ad una depolarizzazione [14].
1.4
Introduzione alla dinamica neuronale
Abbiamo già accennato che l’arrivo di un potenziale di azione dal neurone presinaptico provoca una risposta in tensione (il potenziale postsinaptico) nel potenziale di
membrana del neurone ricevente. A tal proposito si distingue tra potenziale postsinaptico eccitatorio (che ha come acronimo PPSE ) e potenziale postsinaptico inibitorio (che ha come acronimo PPSI ) a seconda che l’effetto sia quello di aumentare o di
diminuire il valore del potenziale di membrana. Analogo significato ha la distinzione
tra sinapsi eccitatoria e sinapsi inibitoria ovvero tra stimolo depolarizzante e stimolo iperpolarizzante. Il numero di contatti sinaptici dipende dal tipo di neurone: ad
esempio i neuroni della corteccia cerebrale (neuroni corticali ) possiedono migliaia
di contatti sinaptici (da 3 · 103 a 104 ) con gli altri neuroni della corteccia dei quali
Figura 1.5. Registrazione di 479 PPSE sul soma di cellule piramidali della corteccia visuale del ratto, in presenza di attività neuronale spontanea (fig.A). Istogramma delle altezze di picco dei PPSE (fig.B) [17].
circa l’85% sono eccitatori ed il resto inibitori. In realtà solo una frazione dell’ordine
del 5-10% risultano sinapsi realmente attive [8, 16]. Per avere un’idea dell’ampiezza
di un PPSE si veda la figura (1.5) in cui sono riportati i PPSE registrati su una
cellula neuronale ed il relativo istogramma delle altezze di picco: come si vede il
valor medio è dell’ordine di 0.5 mV. In figura (1.6) è riportata una rappresentazione
schematica della dinamica neuronale che si instaura in risposta all’arrivo di impulsi
da neuroni presinaptici:
fig.A: un neurone postsinaptico i riceve impulsi da due neuroni presinaptici j = 1,2;
ui (t) e urest rappresentano rispettivamente il potenziale di membrana e il valore
(f )
del potenziale di riposo del neurone i; la quantità ǫi1 (t − t1 ) rappresenta il
(f )
potenziale postsinaptico generato dall’arrivo all’istante t1
di un impulso dal
neurone j = 1;
(f )
fig.B: un impulso che arriva dall’altro neurone presinaptico j = 2 ad un istante t2 ,
entro un intervallo di tempo sufficientemente breve, causa un secondo potenziale postsinaptico che si somma al precedente; in questo regime la risposta
del neurone postsinaptico risulta approssimativamente lineare nel senso che la
risposta è circa proporzionale agli input che riceve;
fig.C: quando ui (t) raggiunge un valore tipico, θ, denominato soglia di attivazione,
il comportamento del neurone diviene altamente non lineare: è generato un
potenziale di azione (il picco dell’impulso rappresentato da una freccia è fuori
dalla scala della figura) che ha una forma stereotipata e quindi senza legame
con gli stimoli che lo hanno prodotto; inoltre il neurone, per tutta la durata
del potenziale di azione, diviene per cosı̀ dire “insensibile”, ovvero refrattario,
agli stimoli che gli arrivano dagli altri neuroni.
La refrattarietà neuronale si distingue in genere in refrattarietà assoluta e refrattarietà relativa. La refrattarietà assoluta è quell’arco temporale (di circa 2ms) corrispondente alla durata del potenziale di azione in cui è impossibile che venga generato
un altro potenziale di azione. La refrattarietà relativa, che segue temporalmente la
refrattarietà assoluta, coincide con la fase di iperpolarizzazione del neurone in cui è
“difficile” ma non impossibile che il neurone venga eccitato fino ad emettere un altro
potenziale di azione. Conseguentemente il periodo di refrattarietà fornisce un limite
inferiore al minimo intervallo temporale tra due potenziali di azione consecutivi.
1.5
La membrana cellulare del neurone
La membrana cellulare del neurone (vedi figura 1.7) è composta da molecole di lipidi
e proteine. Le molecole lipidiche sono disposte in un doppio strato con uno spessore
di circa 6 nm. In questa matrice lipidica si trovano alcune molecole proteiche che
attraversano tutto lo spessore della membrana cellulare entrando quindi in contatto
sia con l’interno della cellula che con il liquido extracellulare. Tali particolari proteine prendono il nome di canali proteici, ovvero canali di membrana, canali acquosi
o canali ionici (la ragione di tali denominazioni sarà chiara a breve). La membrana
cellulare può essere attraversata dalle sostanze dall’esterno all’interno o viceversa
attraverso vari meccanismi. Vi sono ad esempio alcuni tipi di molecole (alcoli o
glicerolo) che attraversano la membrana sciogliendosi nel doppio strato lipidico e
riemergendo dall’altro lato; in tal caso la facilità di penetrazione dipende dal grado
Figura 1.6.
Rappresentazione della dinamica neuronale [15].
di solubilità nei lipidi. Gli ioni inorganici (sodio, potassio, calcio e cloro) che, come
abbiamo già detto, costituiscono le correnti ioniche alla base dell’attività elettrica
neuronale, si muovono attraverso la membrana o legandosi a particolare molecole
dette molecole di trasporto, che li veicolano, ovvero attraverso i canali proteici sopra
citati. Si noti comunque che il meccanismo di trasporto adottato durante la generazione di un potenziale di azione risulta quello dei canali proteici, in quanto i flussi
di ioni coinvolti (dell’ordine di 106 ioni/s) risultano ben oltre le possibilità di azione
delle molecole di trasporto. Nella struttura dei canali proteici (vedi figura 1.7) si
possono riconoscere i seguenti elementi:
• un poro centrale pieno d’acqua;
• una regione del poro che agisce da filtro di selettività regolando il transito degli
Figura 1.7.
a) Struttura della membrana cellulare del neurone; b) struttura di un
canale ionico [14].
ioni in base alle dimensioni ed alle caratteristiche chimico-fisiche;
• un sistema di porte (in inglese gates) che si aprono e si chiudono in modo
stocastico facendo oscillare il canale tra uno stato di apertura ed uno stato
di chiusura; di norma lo stato di chiusura predomina quando il potenziale di
membrana si trova al valore di riposo. 1 .
1.6
Canali ionici e correnti ioniche
Quando il canale ionico si trova in uno stato di apertura il canale è detto attivato,
altrimenti quando si trova in uno stato di chiusura è detto inattivato. È opportuno
sottolineare che essendo l’apertura e chiusura dei canali un processo di natura stocastica l’attivazione o disattivazione di un canale sta a significare solo un’aumentata
o diminuita probabilità di apertura del canale e non uno stato di apertura o chiusura
continua (vedi figura 1.8). Esistono varie modalità di attivazione, ossia di apertura,
di un canale. In particolare se l’apertura del canale può essere regolata dal valore
del potenziale di membrana i canali si dicono voltaggio-attivati. A titolo di esempio citiamo in questa categoria di canali, il canale voltaggio-dipendente del sodio
1
Esiste peraltro l’eccezione costituita da alcuni canali per i quali lo stato di apertura è predominante nella membrana a riposo: si tratta per lo più, come vedremo nel seguito, di quei canali del
cloro e del potassio che risultano responsabili proprio del valore del potenziale di riposo.
Figura 1.8. Esempio di corrente di canale. Come si vede tale corrente risulta di
impulsi di forma quasi rettangolare che possono essere posti in relazione con lo
stato di apertura e chiusura dei canali stessi [19].
che è quello responsabile della depolarizzazione della membrana che provoca la fase
di salita del potenziale di azione. Riguardo alla selettività alla specificità ionica, i
canali si possono distinguere in cationici e anionici a seconda che risultino rispettivamente permeabili agli ioni positivi o negativi. La permeabilità di una membrana
ad una specie ionica, indicata con p, è una proprietà intrinseca della membrana che
misura la “facilità” con cui gli ioni attraversano la membrana stessa; essa è definita
in modo empirico dalla relazione [8, 18]:
J = −p∆[C]
(1.1)
dove J è il flusso molare (misurato in mol/(cm2 ·s)) e ∆[C] rappresenta la differenza
di concentrazione ionica ai due lati della membrana (misurata in mol/cm3 ). P ha
le dimensioni di una velocità ed è solitamente misurata in cm/s. La permeabilità
dipende solo dal tipo e dal numero di canali ionici presenti sulla membrana. In
particolare i canali cationici possono essere specifici o non specifici qualora risultino
o meno specializzati per una particolare specie ionica (ad esempio si hanno canali
specifici del Na+ , K+ , Ca2+ ). I canali anionici risultano essenzialmente costituiti
dai canali del cloro (Cl− ), che è di gran lunga il maggior permeante anionico nelle
soluzioni biologiche.
La conduttanza è invece una misura dell’abilità della membrana di trasportare corrente elettrica ed è misurata solitamente in Siemens, con simbolo S, dove 1S = 1Ω −1 .
Poiché la corrente è trasportata dagli ioni, la conduttanza di una membrana non
dipenderà solo dalle proprietà della membrana (cioè dalla permeabilità) ma anche
dalla concentrazione ionica all’interno ed all’esterno della cellula (ovvero il numero
dei portatori liberi di carica). Non è tuttavia possibile ricavare una relazione matematica generale tra permeabilità e conduttanza perché tale relazione dipende strettamente dalle modalità con cui gli ioni attraversano il canale (semplice diffusione
attraverso i pori pieni d’acqua ovvero modelli più complicati che analizzano l’interazione canale-ione permeante). In generale quindi la corrente che attraversa un
canale ionico dipenderà [14, 20, 18]):
• dalla conduttanza del canale;
• dal gradiente di concentrazione tra l’interno e l’esterno della cellula che tende
a produrre un flusso dalla zona a maggior concentrazione a quella a minor
concentrazione secondo la legge empirica enunciata da Fick [18]:
Jdif f = −D
d[C]
dx
(1.2)
dove Jdif f rappresenta il flusso dovuto alla diffusione (misurato in numero di
ioni/(cm2 ·s)), D è il coefficiente di diffusione (misurato in cm2 /s) e [C] è la
concentrazione ionica (qui espressa in numero di ioni/cm3 );
• dalla differenza di potenziale applicata alla membrana.
1.7
1.7.1
Origine del potenziale di riposo
Un modello cellulare semplificato
In figura (1.9) è presentato un modello cellulare semplificato [14] ma che coglie
l’essenza dell’origine del potenziale di riposo della cellula neuronale. La cellula contiene ioni potassio (K + ), sodio (Na+ ), cloro (Cl− ) ed altri anioni (A− ) di grandi
dimensioni ed è a sua volta immersa in una soluzione di sodio, potassio e cloro. Le
Figura 1.9. Un modello semplificato per le distribuzioni ioniche all’interno ed
all’esterno della cellula. Le frecce rappresentano le direzioni dei gradienti di concentrazione ed elettrici per il potassio (K + ) e per il cloro (Cl− ). Le concentrazioni
sono espresse in millimoli per litro [14].
concentrazioni ioniche mostrate in figura sono espresse in millimoli per litro (che ha
per simbolo mM dove 1mM = 10−3 mol/l). Nelle cellule neuronali sono presenti
altri ioni, come il calcio e il magnesio, ma il loro contributo al potenziale di riposo
è trascurabile. In questo modello la membrana cellulare è completamente impermeabile al sodio ed all’anione interno (A− ) e risulta invece permeabile al potassio
ed al cloro. Il potassio risulta più concentrato dentro la cellula che fuori e tende
quindi a muoversi verso l’esterno secondo il proprio gradiente di concentrazione.
D’altro canto, come abbiamo precedentemente illustrato, la superficie interna della
membrana è negativa rispetto a quella esterna, e quindi il gradiente di potenziale
tende ad attrarre il potassio dentro la cellula. In una cellula a riposo il gradiente di
concentrazione ed il gradiente elettrico sono in equilibrio. Si definisce potenziale di
equilibrio di una specie ionica il valore del potenziale di membrana al quale non si ha
alcun flusso netto di quella specie ionica. Per il cloro il gradiente di concentrazione
ed il gradiente elettrico hanno direzione opposta rispetto al potassio.
1.7.2
L’equazione di Nerst
Il potenziale di equilibrio di ogni specie ionica è legato alle concentrazioni intracellulari ed extracellulari attraverso la cosiddetta equazione di Nerst:
Eione =
kB T [n]e
ln
q
[n]i
(1.3)
dove: Eione è il potenziale di equilibrio dello ione; [n]e , [n]i sono rispettivamente le
concentrazioni extracellulari ed intracellulari; kB ≃ 1.38 · 10−23 J/K è la costante
di Boltzmann; T è la temperatura assoluta in Kelvin; q è la carica elettrica (in
Coulomb) della specie ionica. È possibile capire l’origine dell’equazione di Nerst
attraverso il seguente ragionamento (vedi anche figura 1.10). Dalla meccanica sta′
tistica di Boltzmann per sistemi in equilibrio termico si ha che la probabilità p(U <
′
′
′
U < U + dU) che una molecola si trovi in uno stato di energia U < U < U + dU
′
′
risulta: p(U < U < U + dU) ∝ exp(−U/kB T ) [21]. Consideriamo adesso degli
ioni con carica positiva q in un campo elettrico statico. La loro energia nel punto
x risulta U(x) = qV (x) dove V (x) è il potenziale nel punto x. La probabilità di
trovare uno ione in una regione nell’intorno del punto x è perciò proporzionale alla
quantità exp(−qV (x)/kB T ). Reinterpretando la densità di probabilità come una
quantità proporzionale ad una densità ionica [n(x)], ovvero ad una concentrazione,
si ha:
p(U(x1 ))
[n(x1 )]
=
= exp(−q(V (x1 ) − V (x2 ))/kB T )
p(U(x2 ))
[n(x2 )]
(1.4)
e dunque all’equilibrio termodinamico si ha che un gradiente di potenziale elettrostatico ∆V = (V (x1 ) − V (x2 )) genera un gradiente di densità ionica . Ma poiché
questo è un assunto su uno stato di equilibrio la relazione deve valere anche nell’altro senso: ossia un gradiente di concentrazione genera un gradiente di potenziale
elettrostatico. Risolvendo la (1.4) rispetto al gradiente di potenziale si ha che all’equilibrio termodinamico vale ∆V =
kB T
q
2
ln [n]
che è appunto l’equazione di Nerst.
[n]1
La quantità kB T /q ha le dimensioni di una differenza di potenziale elettrico e per
Figura 1.10.
Origine del potenziale di Nerst [15].
una specie ionica monovalente (per la quale q = e, dove e ≃ 1.6 · 10−19 C è il valore
assoluto della carica dell’elettrone) è uguale a circa 25 mV a temperatura ambiente
(T ≃ 300 K). Per il modello cellulare mostrato in figura (1.9) nel quale il rapporto delle concentrazioni del cloro e del potassio è uguale e pari a 1:30 si avrà a
T ≃ 300 K: Ek ≃ −85 mV , ECl ≃ −85 mV . Nel modello cellulare semplificato,
essendo gli ioni potassio e cloro gli unici in grado di muoversi attraverso la membrana ed essendo entrambi in equilibrio a -85mV, la cellula non manifesta alcun
guadagno o perdita netta di ioni: il potenziale di riposo della cellula semplificata
coincide quindi con il potenziale di equilibrio del potassio e del cloro.
1.7.3
Effetto del sodio e pompe ioniche
Lo ione sodio (Na+ ) è molto più concentrato all’esterno che all’interno della cellula (vedi figura 1.9), dunque per opporsi all’ingresso del sodio dovuto al gradiente
di concentrazione la membrana deve avere una differenza di potenziale tra l’interno e l’esterno positiva: infatti usando le concentrazioni di figura (1.9) si ha che a
T ≃ 300 K il potenziale di equilibrio del sodio risulta EN a ≃ +34 mV . Dunque in
una cellula neuronale, dove il potenziale di riposo della membrana è negativo, sia
il gradiente di concentrazione, sia il potenziale di membrana favoriscono l’ingresso
del sodio. La membrana cellulare è scarsamente permeabile al sodio ma il sia pur
Figura 1.11.
Flussi ionici passivi e pompe ioniche in una cellula in stato
stazionario [14].
limitato ingresso di questo ione depolarizza leggermente la membrana rispetto al
potenziale di equilibrio del potassio, con la conseguenza che il potassio, fuori dall’equilibrio, fluisce verso l’esterno. Per mantenere lo stato di equilibrio (ovvero le
concentrazioni ioniche costanti) a fronte di queste perdite continue esistono delle
cosiddette pompe ioniche che trasportano il sodio fuori dalla cellula ed il potassio
dentro la cellula in modo da mantenere uno stato stazionario, ovvero una situazione
di equilibrio dinamico. Il più importante sistema di trasporto è costituito dalla pompa Na-K che trasporta tre ioni sodio fuori dalla cellula per ogni due ioni potassio
portati invece all’interno: in tal caso si dice che il rapporto di accoppiamento Na:K
della pompa è di 3:2. Tale situazione è rappresentata in figura (1.11) dove le frecce
tratteggiate indicano i movimenti ionici passivi (ovvero guidati solo dal bilancio tra
i gradienti elettrici e di concentrazione) mentre le frecce continue e i circoli indicano
le pompe ioniche. La lunghezza delle frecce indica l’entità dei movimenti netti ionici:
per ciascuno ione il flusso totale è nullo all’equilibrio.
1.7.4
Effetto della permeabilità ionica e dei meccanismi di
trasporto
Abbiamo visto nel paragrafo 1.7.2 che il potenziale di riposo della membrana è
determinato principalmente dal rapporto delle concentrazioni transmembranali del
potassio. Esiste tuttavia una dipendenza non solo dalle concentrazioni ioniche ma
anche dalla permeabilità alle specie ioniche. L’equazione di campo costante, detta
anche equazione GHK dagli autori D.E. Goldman [22], A.L. Hodgkin e B. Katz [23],
esprime tale dipendenza:
Eriposo =
kB T pk [K + ]e + pN a [Na+ ]e + pCl [Cl− ]i
;
ln
e
pk [K + ]i + pN a [Na+ ]i + pCl [Cl− ]e
(1.5)
dove Eriposo è il potenziale di riposo della membrana; e (valore assoluto della carica dell‘elettrone) indica la carica degli ioni monovalenti; il simbolo [I]j , dove I =
K + ,Na+ ,Cl− e j = i,e, indica la concentrazione interna ed esterna delle specie
ioniche; pk , pN a , pCl rappresentano le permeabilità ioniche di ogni ione.
Tale
equazione è basata sul presupposto che, a potenziale costante, non deve cambiare
la carica sulla membrana anche se gli ioni la attraversano in piccole quantità. Di
conseguenza le correnti trasportate dalle perdite di sodio verso l’interno, di potassio
verso l’esterno e dalle altre perdite del cloro devono dare come somma zero. Altrimenti si determinerebbe un accumulo, o una perdita, costante di carica e quindi una
deriva costante del potenziale di membrana. Il nome equazione di campo costante
è legato al fatto che una delle ipotesi alla base di essa è che il campo elettrico all’interno della membrana sia uniforme. Come si vede l’equazione ricorda quella di
Nerst ma considera tutte le specie ioniche presenti “pesate” con la loro permeabilità
e corrisponde pertanto a quello che intuitivamente era possibile aspettarsi: ovvero
che il potenziale di membrana tende tanto più al valore del potenziale di equilibrio
di una specie ionica quanto più la sua permeabilità è maggiore di quella delle altre
specie ioniche. È possibile dimostrare [14] che non vi è una grossa dipendenza del
potenziale di riposo dal cloro e pertanto il suo contributo è spesso trascurato; in tal
caso l’equazione di campo costante viene cosı̀ riscritta:
Eriposo =
kB T [K + ]e + b[Na+ ]e
;
ln
e
[K + ]i + b[Na+ ]i
(1.6)
dove b = pN a /pk . Una descrizione ancora più accurata è fornita dall’equazione di
stato stazionario [24] che considera anche gli effetti dei processi di trasporto attivo
della pompa ionica Na − K:
Eriposo =
kB T r[K + ]e + b[Na+ ]e
;
ln
e
r[K + ]i + b[Na+ ]i
(1.7)
dove r è il rapporto di accoppiamento del sistema di trasporto (nel caso della pompa Na − K si ha r = 3/2). Si capisce facilmente come gli effetti della pompa
si ripercuotano sul potenziale di membrana: infatti il diverso flusso di ioni Na+
e K + (tre ioni sodio fuori dalla cellula per ogni due ioni potassio portati invece
all’interno) causato dalla pompa genera una corrente ionica netta verso l’esterno;
questo flusso di cariche positive verso l’esterno tende a iperpolarizzare la membrana
ad un valore leggermente più negativo (ossia avvicina il potenziale di membrana
un po’ di più al potenziale di equilibrio del potassio) di quello che ci si aspetterebbe solo in base a meccanismi passivi. Per avere un’idea dell’entità del contributo delle pompe ioniche si confronti il valore del potenziale di riposo predetto
dall’equazione di campo costante e dall’equazione di stato stazionario relativamente
ad assoni di calamaro in acqua di mare alla temperatura di T ≃ 300 K: usando l’equazione di campo costante si trova Eriposo ≃ −67 mV , mentre usando l’equazione
di stato stazionario si trova Eriposo ≃ −73mV (abbiamo usato i seguenti valori realistici: [K + ]i = 400mM, [K + ]e = 10mM, [Na+ ]i = 50mM, [Na+ ]e = 460mM,
b = pN a /pk = 0.04, r = 1.5).
1.8
Proprietà elettriche passive della membrana
Da un punto di vista elettrico la più semplice schematizzazione di una porzione di
membrana cellulare a riposo fa ricorso a tre elementi circuitali: una resistenza (Rm ),
una capacità (Cm ), ed un generatore di tensione V uguale al potenziale di riposo
(vedi figura 1.12 e figura 1.13). La presenza della resistenza si spiega con l’esisten-
Figura 1.12.
Schematizzazione elettrica di una porzione di membrana cellulare
del neurone. Eriposo indica il potenziale di riposo [8].
Figura 1.13. Equivalente circuitale dell’intera membrana cellulare. I simboli Rm e
Cm in questo caso rappresentano il parallelo rispettivamente di tutte le resistenze
e le capacità delle singole porzioni di membrana; Eriposo indica il potenziale di
riposo; Iin rappresenta una corrente iniettata dentro la cellula [8].
za dei canali ionici che realizzano un contatto tra l’interno e l’esterno della cellula.
La resistenza di membrana è di solito riportata come una resistenza di membrana
specifica, rm , definita come una resistenza per unità di superficie (in unità Ω · cm2 ).
rm è quindi ottenuta dividendo Rm per l’area della membrana considerata. rm è determinata principalmente dalle permeabilità a riposo del potassio e del cloro. Valori
tipici di rm variano da circa 103 Ω · cm2 per membrane con molti canali ionici a
circa 5 x 104 Ω · cm2 per membrane con pochi canali ionici. Ma oltre a permettere il
passaggio di correnti ioniche, la membrana accumula cariche sulla superficie interna
ed esterna, ed è proprio questa separazione che detemina il potenziale di membrana.
La realizzazione di questa separazione di cariche conferisce alla membrana le proprietà di un condensatore. La capacità di membrana è di solito specificata in termini
di una capacità di membrana specifica, cm , definita come una capacità per unità
di superficie (in unità F/cm2 ). Cm è quindi ottenuta moltiplicando cm per l’area
della membrana considerata. cm è tipicamente dell’ordine di 1 µF/cm2 . Tramite
la relazione qm = cm V , dove qm è la quantità di carica per unità di superficie, ed
assumendo V ≃ -65mV si ha che qm ≃ (1µ F/cm2 ) x (65mV) ≃ 6.5 x 10−8 C/cm2
che equivale, dividendo per il valore assoluto della carica dell’elettrone, a circa 4
x 1011 ioni monovalenti per cm2 . Ci preme sottolineare che tale schematizzazione
descrive solo il comportamento passivo della membrana e non prende in considerazione eventuali componenti non lineari o attivi come ad esempio conduttanze
voltaggio-dipendenti.
Capitolo 2
Modelli semplificati di neuroni
Nella prima parte di questo capitolo introduciamo il primo modello realistico di
neurone, sviluppato nel 1952 da Hodgkin e Huxley per l’assone gigante del calamaro, che valse loro il premio Nobel per la medicina nel 1963. Hodgkin e Huxley
derivarono il loro modello in maniera fenomenologica, in modo da poter riprodurre
la fisiologia dell’assone gigante del calamaro e gli andamenti sperimentali non lineari
delle conduttanze associate alle correnti ioniche di membrana. Alcuni dei primi studi
sui potenziali di equilibrio per le varie specie ioniche furono fatti sull’assone gigante
del calamaro perché questo ha un diametro dell’ordine di 1 mm ed è dunque molto
grande rispetto al soma del neurone di un mammifero, che è dell’ordine di 70 µm,
quindi si presta meglio a studi di elettrofisiologia. Il modello di Hodgkin-Huxley
riproduce la dinamica del potenziale di membrana e il meccanismo di generazione
dei potenziali di azione, nonché l’andamento delle principali correnti ioniche di membrana. Tale modello è considerato il modello quantitativo che ha avuto il maggior
successo nelle neuroscienze: le schematizzazioni sviluppate da Hodgkin e Huxley per
l’assone gigante del calamaro hanno trovato negli anni passati e trovano anche oggi,
applicazione in centinaia di modelli per neuroni delle più diverse tipologie.
In questo capitolo inoltre spieghiamo come combinare tutti gli elementi costitutivi di un neurone (dendriti, sinapsi, conduttanze dipendenti dal potenziale, assoni)
al fine di ottenere un semplice modello funzionale della singola cellula. Questa operazione di semplificazione trascura la struttura dei dendriti e sostituisce la descrizione
dei processi di emissione dei potenziali di azione fondata sulle conduttanze (ovvero
la descrizione fornita dalle equazioni realistiche di Hodgkin-Huxley per le correnti di
membrana), con una descrizione basata sull’utilizzo di modelli formali, come il modello leaky integrate-and-fire 1, che tratteremo in dettaglio. Questo modello descrive
in modo estremamente semplificato la dinamica sottosoglia, cioè la dinamica prima
dell’emissione di un potenziale di azione, mentre il potenziale di azione è descritto sinteticamente come un evento stereotipato. In questo modo possiamo ridurre
notevolmente la complessità del problema e cosı̀ caratterizzare il comportamento dinamico dei neuroni attraverso una singola equazione differenziale ordinaria piuttosto
che tramite un sistema di più equazioni non lineari accoppiate. Tali semplificazioni
ci permettono di effettuare simulazioni numeriche di reti contenenti molti neuroni
del tipo leaky integrate-and-fire, data la rapidità di evoluzione del modello. Nei
prossimi capitoli tratteremo cosı̀ reti formate da un gran numero di neuroni interconnessi, al fine di simularne la dinamica e di analizzare la nascita e la stabilità di
soluzioni collettive non banali. La comprensione di un qualsiasi sistema complesso
passa per la scelta di un livello di descrizione che afferri le proprietà fondamentali
del sistema e trascuri quelle non essenziali allo scopo proposto.
1
Nel proseguo della tesi useremo questi anglicismi invece dei corrispondenti termini italiani
perché, ormai, sono invalsi nel linguaggio comune.
2.1
Dal modello di Hodgkin-Huxley al modello
leaky integrate-and-fire
Il modello di Hodgkin-Huxley è un modello realistico a quattro dimensioni (in cui
cioè la dinamica del neurone è descritta da quattro variabili), pensato per riprodurre
i dati sperimentali relativi ad una particolare fibra nervosa: l’assone gigante del
calamaro [25, 26]. Il modello matematico che L. Hodgkin e A. F. Huxley formularono
valse loro il premio Nobel per la medicina nel 1963 e rappresenta ancora un modello
attuale per lo studio della dinamica del singolo neurone. In particolare, questo
modello è costituito da un sistema di quattro equazioni differenziali del primo ordine
che descrivono la dinamica del potenziale di membrana e delle tre correnti ioniche
fondamentali: la corrente del sodio (IN a ), la corrente del potassio (IK ) e la corrente
di perdita, o di dispersione, (IL dall’inglese leakage current), dovuta principalmente
al cloro (Cl− ), ma che riassume anche l’effetto di altre specie ioniche minoritarie,
che non vengono descritte esplicitamente. Il meccanismo alla base di queste correnti
ioniche risiede nel fatto che le conduttanze della membrana cellulare per il sodio
(gN a ) e per il potassio (gK ) sono dipendenti dalla differenza di potenziale applicata
alla membrana, in particolare la probabilità che i canali si aprano aumenta con
la depolarizzazione della membrana. L’apertura dei canali per i vari ioni avviene
tuttavia con tempi e modalità diverse: la depolarizzazione della membrana attiva
inizialmente un aumento della conduttanza del sodio (seguita da una sua successiva
inattivazione) e solo con un certo ritardo temporale viene attivata la conduttanza
del potassio. Inoltre l’effetto sul potenziale di membrana dovuto all’aumento della
conduttanza è diverso per il sodio e per il potassio:
• per quanto riguarda il sodio si ha un processo di retroazione positiva; infatti
una piccola depolarizzazione aumenta il numero di canali aperti e questo, a
sua volta, dà luogo ad un ulteriore ingresso del sodio secondo il gradiente
Figura 2.1. Fase di salita del potenziale di azione. I segni + di colore nero indicano gli ioni N a+ che entrano nella cellula. Il gradino di tensione depolarizza la
membrana e fa aprire i canali sodio (li attiva); questo causa l’entrata del N a+ nella
cellula e ciò aumenta la depolarizzazione inducendo l’aumento della differenza di
potenziale fra l’interno e l’esterno della cellula.
elettrochimico e ad una depolarizzazione ancor più grande;
• per quanto riguarda il potassio, si ha invece che il flusso in uscita secondo
il gradiente elettrochimico, dovuto alla depolarizzazione, porta alla ripolarizzazione della membrana e quindi alla conseguente riduzione della conduttanza
fino al suo valore di riposo (retroazione negativa).
Il profilo tipico di un potenziale di azione è quindi spiegabile, per quanto riguarda
la fase di salita, con un improvviso grande aumento della permeabilità di membrana
al sodio (vedi figura 2.1); la conseguente corrente del sodio porta rapidamente il
potenziale di membrana a spostarsi verso il potenziale di equilibrio del sodio stesso
(EN a = 55 mV ).
La fase di caduta del potenziale di azione, ovvero la ripolar-
izzazione della membrana, è dovuta invece ad un successivo aumento della permeabilità al potassio (vedi figura 2.2): a causa della corrente ionica del potassio, il
potenziale di membrana si sposta questa volta, verso il potenziale di equilibrio del
potassio (Ek = −75 mV ). Si ha infine una fase di rilassamento del potenziale verso
il suo valore di riposo (Eriposo = −70 mV ).
Figura 2.2. Fase di caduta del potenziale di azione. I segni + di colore nero
indicano gli ioni N a+ , mentre i segni + di colore verde indicano gli ioni K + che
lasciano la cellula. Alla depolarizzazione segue infatti una inattivazione dei canali
N a; i canali K sono attivati con un certo ritardo e questo causa la fuoriuscita degli
ioni K + e la ripolarizzazione della membrana.
Figura 2.3. Ricostruzione teorica dell’andamento del potenziale d’azione e delle
relative variazioni della conduttanza del sodio gN a e del potassio gK in funzione
del tempo [14].
Il modello di Hodgkin-Huxley spiega inoltre l’esistenza di un livello di soglia
del potenziale di membrana al di sopra del quale viene emesso l’impulso, senza
richiedere alcuna discontinuità nella conduttanza del sodio (gN a ) o in quella del
potassio (gK ). Il fenomeno può essere compreso se immaginiamo di far passare una
corrente attraverso la membrana depolarizzandola solo sino alla soglia (Esoglia =
−55 mV ) e poi di interrompere la corrente. Essendo il potenziale di membrana
lontano dal potenziale di equilibrio del potassio, vi sarà un aumento della corrente
di potassio in uscita, ma verranno attivati anche alcuni canali di sodio, aumentando
la corrente di sodio in ingresso. Alla soglia questi aumenti di corrente sono uguali e
opposti (si ha un equilibrio dinamico), ma la conduttanza del sodio ora è instabile.
Infatti se nella cellula entra un solo ione di sodio in più, la depolarizzazione aumenta,
gN a aumenta, entra altro sodio e si innesca la retroazione positiva. Se d’altra parte
uno ione in più di potassio lascia la cellula, la depolarizzazione diminuisce, gN a
diminuisce, la corrente di sodio diminuisce e la prevalenza della corrente di potassio
determina la ripolarizzazione. Man mano che il potenziale di membrana si avvicina
al proprio livello di riposo, la corrente di potassio diminuisce poi fino ad eguagliare
nuovamente la corrente a riposo del sodio diretta verso l’interno. Riassumendo, la
depolarizzazione oltre la soglia determina un aumento di gN a sufficiente a innescare il
processo che porta all’emissione di un potenziale di azione, mentre depolarizzazioni
appena più deboli portano il potenziale di membrana a rilassarsi verso il suo valore
di riposo.
Un ultimo aspetto spiegabile con questo modello è il tempo di refrattarietà; come
già detto nel paragrafo (1.4), dopo l’emissione di un potenziale di azione abbiamo a
che fare con due periodi diversi di retrattarietà: il periodo di refrattarietà assoluto
e quello relativo. Il periodo refrattario assoluto coincide essenzialmente con l’intera
durata del potenziale di azione ed è causato dall’inattivazione dei canali Na+ che in
precedenza si erano aperti per depolarizzare la membrana; questi canali rimangono
inattivi finché la membrana non si ripolarizza, dopodiché si chiudono e si riattivano
riacquistando cosı̀ la loro capacità di aprirsi in risposta ad uno stimolo. Il periodo
refrattario relativo è successivo a quello assoluto; i canali potassio si aprono per terminare il potenziale di azione ripolarizzando la membrana, dunque la conduttanza
di membrana del potassio cresce drasticamente. Gli ioni K + che fluiscono in gran
numero fuori dalla cellula fanno sı̀ che il potenziale di membrana si avvicini molto al
potenziale di equilibrio del potassio; questo determina una breve iperpolarizzazione
della membrana, cosicché il potenziale di membrana diventa più negativo dell’usuale
potenziale di riposo (Eriposo = −70 mV ). Quindi, finché la conduttanza del potassio non ritorna di nuovo al suo valore di riposo, è necessario uno stimolo maggiore
per raggiungere il valore di soglia e dar vita ad una seconda depolarizzazione. Il
raggiungimento del potenziale di equilibrio di riposo determina la fine del periodo
di refrattarietà relativo.
Un neurone dunque genererà un potenziale di azione quando il suo potenziale di
membrana raggiungerà un valore di soglia compreso tra −55 e −50 mV . Durante
l’emissione del potenziale di azione, il potenziale di membrana descresce rapidamente e assume un valore che è iperpolarizzato rispetto al potenziale di soglia. Il
meccanismo per cui le conduttanze dipendenti dal potenziale K + e Na+ producono
dei potenziali di azione è ben compreso e modellizzabile accuratamente per il neurone del calamaro gigante.
D’altra parte, come vedremo nel paragrafo successivo, i modelli dei neuroni possono
essere semplificati se non vengono esplicitamente inclusi i meccanismi biofisici responsabili dei potenziali di azione. I modelli integrate-and-fire nascono da questa
semplificazione supponendo che il potenziale di azione sia generato ogni volta che il
potenziale di membrana del neurone modello raggiunge un valore di soglia Θ; dopo
l’emissione del potenziale di azione, al potenziale viene riassegnato un valore R inferiore al potenziale di soglia, R < Θ. Tali modelli formali partono dal presupposto
che un potenziale di azione costituisca un evento stereotipato, per cui viene descritta solo la dinamica sottosoglia da un’unica variabile che rappresenta il potenziale
di membrana (modello unidimensionale). Inoltre questi modelli non riproducono in
modo dettagliato i potenziali di azione né includono l’effetto di adattamento o il
tempo di refrattarietà. L’insorgenza del potenziale di azione è cosı̀ caratterizzata
solo dal tempo di sparo (o in inglese firing time).
2.2
Neuroni leaky integrate-and-fire
Il modello integrate-and-fire è stato proposto da Lapicque nel 1907 [27], molto prima
che fosse compreso il meccanismo di generazione dei potenziali di azione; nonostante
la sua semplicità, questo modello rappresenta tuttora una descrizione estremamente
utile dell’attività neuronale. Non volendo fornire una descrizione biofisica del potenziale di azione, a questi modelli rimane il compito, più semplice, di modellizzare la dinamica del potenziale di membrana sottosoglia. Questo compito può esser svolto con
vari livelli di rigore; nella versione più semplice, sono ignorate tutte le conduttanze di
membrana attive, compresi gli input sinaptici, e l’intera conduttanza di membrana
è schematizzata con un singolo termine di perdita, passivo, im = ḡL(V − EL ), con
im corrente di membrana, V potenziale di membrana, EL potenziale di riposo e ḡL
che rappresenta una conduttanza efficace di membrana a riposo. Questa versione è
denominata passiva o modello leaky integrate-and-fire (al quale ci riferiremo anche
come LIF). Sperimentalmente è noto che le conduttanze neuronali sono approssimativamente costanti per piccole fluttuazioni attorno al potenziale di membrana di
riposo; il modello LIF assume che questa costanza si mantenga nell’intero intervallo
di variazione del potenziale sottosoglia. Per alcuni neuroni, questa si rivela un’approssimazione ragionevole, mentre per altri meno.
Con queste approssimazioni il neurone si comporta come un circuito elettrico costituito da una resistenza ed una capacità in parallelo (figura 2.4) ed il potenziale di
membrana si determina cosı̀ attraverso l’equazione
cm
dV
Ie
= −im +
dt
A
(2.1)
dove cm è la capacità per unità di superficie della membrana, A è la superficie della
membrana, im è la corrente di membrana per unità di superficie ed Ie è la corrente
esterna iniettata nel neurone. Con im = ḡL (V − EL ) si ha infine
cm
dV
Ie
= −ḡL (V − EL ) + .
dt
A
(2.2)
È conveniente moltiplicare l’equazione (2.2) per la resistenza specifica di membrana
Figura 2.4.
Circuito equivalente per il modello di neurone. [15].
rm , data in questo caso da rm = 1/ḡL ; questo cancella il fattore ḡL nel membro a
destra dell’equazione e lascia un fattore cm rm = τm nel membro di sinistra, dove τm
è la costante di tempo di membrana del neurone. L’ultimo termine del membro di
destra diviene rm /A = Rm , dove Rm è la resistenza di membrana totale. Si arriva
cosı̀ all’equazione fondamentale per i modelli leaky integrate-and-fire:
τm
dV
= EL − V + Rm Ie .
dt
(2.3)
Per completare la dinamica del modello LIF occorre aggiungere una regola “ad
hoc”: riassegnare al potenziale il valore R ogniqualvolta il potenziale V raggiunga
il valore di soglia e venga emesso un potenziale di azione. L’equazione (2.3) mostra
che, quando Ie = 0, il potenziale di membrana si rilassa esponenzialmente con una
costante di tempo τm a V = EL ; EL è dunque il potenziale di riposo della cellula
modello.
Il potenziale di membrana per il modello passivo integrate-and-fire è determinato
integrando l’equazione (2.3) e applicando la regola aggiuntiva riguardo alla soglia
ed alla riassegnazione del valore del potenziale per la generazione del potenziale di
azione. In figura (2.5) è mostrata la risposta di un neurone LIF ad una corrente
esterna che varia nel tempo.
Figura 2.5. Modello leaky integrate-and-fire guidato da una corrente esterna che
varia temporalmente. Il grafico superiore indica il potenziale di membrana, mentre
quello inferiore la corrente applicata. I potenziali d’azione sono semplicemente
sovrapposti alla traiettoria del potenziale di membrana ogniqualvolta il potenziale
raggiunga il valore di soglia. [9].
La frequenza d’emissione dei potenziali d’azione di un modello LIF in risposta
ad una corrente iniettata costante può essere calcolata analiticamente. Quando Ie è
indipendente dal tempo, il potenziale sottosoglia V (t) può essere facilmente calcolato
risolvendo l’equazione (2.3):
V (t) = EL + Rm Ie + (V (0) − EL − Rm Ie )exp(−t/τm ),
(2.4)
dove V (0) è il valore di V al tempo t = 0. Questa equazione è valida per il modello
passivo solo finché V rimane sottosoglia. Supponiamo che a t = 0 il neurone abbia
appena emesso un potenziale di azione e si abbia quindi V (0+ ) = R; il potenziale
di azione successivo verrà emesso quando il potenziale di membrana raggiungerà il
valore di soglia Θ, cioè, ad un tempo t = tisi dove
V (tisi ) = Θ = EL + Rm Ie + (R − EL − Rm Ie )exp(−tisi /τm ).
(2.5)
Risolvendo per tisi , ovvero per il tempo a cui si ha il potenziale di azione successivo,
possiamo determinare l’intervallo tra uno sparo e l’altro (in inglese interspike interval
o ISI) per una corrente Ie costante, o, equivalentemente, il suo inverso, che possiamo
chiamare frequenza d’emissione dei potenziali d’azione del neurone,
risi
1
Rm Ie + El − R
=
= τm ln(
)
tisi
Rm Ie + EL − Θ
−1
.
(2.6)
Questa espressione è valida se Rm Ie > Θ − EL , altrimenti risi = 0. Per valori
sufficientemente grandi di Ie , possiamo espandere al primo ordine l’equazione (2.6)
ed ottenere
risi
"
#
Rm Ie + El − Θ
≈
,
τm (Θ − R)
(2.7)
che mostra come la frequenza di emissione cresca linearmente con Ie per grandi
valori di Ie .
La figura (2.6A) mostra che la frequenza di emissione dei potenziali di azione,
determinata come l’inverso dell’intervallo temporale tra i primi due impulsi emessi
da un neurone corticale in vivo in risposta ad una corrente iniettata (cerchi pieni), è
in accordo con i risultati ricavati dal modello LIF, anche se il neurone reale esibisce
una caratteristica di adattamento della frequenza di emissione prima di raggiungere
uno stato stazionario (figura 2.6B), che non è inclusa in questa semplice versione del
modello.
2.2.1
Correnti sinaptiche
Nel caso in cui il neurone riceva degli impulsi da altri neuroni, la cosa si può schematizzare nell’ambito dei modelli LIF sostituendo alla corrente esterna Ie , che compare
Figura 2.6. (A) Confronto delle frequenze di emissione dei potenziali d’azione in
funzione della corrente iniettata, calcolate l’una con il modello integrate-and-fire,
l’altra attraverso le misure su un neurone corticale in vivo. I punti derivano da
una cellula piramidale nella corteccia visiva primaria di un gatto. I cerchi pieni
mostrano l’inverso dell’ISI per i primi due impulsi emessi, mentre i cerchi vuoti
mostrano la frequenza di emissione degli impulsi nello stato quasi stazionario, dopo
l’adattamento della frequenza stessa. (B) Registrazione dell’attività di un neurone
corticale, soggetto ad una corrente iniettata costante, in cui è visibile l’adattamento della frequenza di emissione. (C) Traiettoria del potenziale di membrana e
potenziali di azione per un modello integrate-and-fire con una corrente aggiuntiva
Ia (vedi paragrafo 2.2.2). [9].
nell’equazione (2.3), la corrente sinaptica Isin . In particolare l’effetto prodotto da
un solo impulso ricevuto dal neurone al tempo t corrisponde ad una corrente postsinaptica che si può scrivere nel seguente modo:
Isin = −Gm [V + W ]τm δ(t)
(2.8)
per una sinapsi che risponda in modo infinitamente rapido [28]. In questa equazione
Gm = 1/Rm è la conduttanza di membrana, mentre W è il potenziale di inversione
della sinapsi il cui segno determina se l’effetto dell’impulso è eccitatorio o inibitorio.
Dato che il potenziale di membrana V ha segno negativo, la sinapsi è detta eccitatoria
(rispettivamente inibitoria) se W < 0 (W > 0); il segno di V è all’origine anche del
segno negativo nell’equazione (2.8). Nel caso in cui il neurone sia connesso ad altri
N neuroni pre-sinaptici il modello LIF si può riscrivere come
τm V̇ = EL − V − τm (V + W )
(k)
dove il tempo tj
N X
X
j=1 k
(k)
δ(t − tj ) ,
(2.9)
rappresenta l’istante di ricezione dell’impulso k-esimo emesso dal
j-esimo neurone pre-sinaptico.
-50
Θ
-52
-54
V
-56
-58
R
-60
150
175
tempo
200
Figura 2.7. Andamento temporale del potenziale di membrana per un neurone
LIF soprasoglia in assenza di stimoli presinaptici. Le frecce indicano l’istante in
cui avviene l’emissione di un potenziale di azione.
Un modello ancora più semplificato, ma largamente usato in letteratura e che
mette in connessione la dinamica del modello LIF con quella di oscillatori di fase è
il seguente [6]
v̇ = a − v −
N X
X
j=1 k
(k)
δ(t − tj ) ,
(2.10)
dove si è assunto che EL = 0, che il tempo unitario sia τm e che il potenziale di
membrana sia stato riscalato come v = (V − R)/(Θ − R), in modo che il valore di
soglia sia 1, mentre il valore di riazzeramento sia 0, quindi v ∈ [0,1]. Nell’equazione
(2.10) il termine a rappresenta una corrente esterna adimensionale. In assenza di
stimoli esterni, la soluzione dell’equazione (2.10) è semplicemente v(t) = a(1 −
exp(−t)), quindi se a < 1 il suo valore asintotico resta sempre sottosoglia (essendo
la soglia posta ad 1), altrimenti se a > 1 il potenziale di membrana raggiunge soglia
e viene riazzerato in modo ripetitivo con periodo tisi = ln[(a − 1)/a]. In questo
ultimo caso il neurone è detto soprasoglia e la sua dinamica ricorda quella di un
semplice oscillatore armonico sovrasmorzato. Tale dinamica è riportata in figura
(2.7). Questo modello sarà oggetto degli studi sviluppati nel cap.4.
2.2.2
Adattamento della frequenza di emissione degli impulsi e refrattarietà
L’adattamento della frequenza di emissione dei potenziali d’azione è una caratteristica comune dei neuroni piramidali della corteccia celebrale dei mammiferi e consiste
nell’allungamento degli ISI col passare del tempo in presenza di una corrente costante
iniettata nella cellula, sino a giungere ad una frequenza di emissione stazionaria (vedi figura 2.6). La considerazione di questo fenomeno ci permette di mostrare come
un modello LIF possa essere modificato per incorporare una dinamica più complessa. Il modello LIF che abbiamo descritto nel paragrafo precedente è basato su
due approssimazioni distinte: una descrizione altamente semplificata del potenziale
di azione e l’assunzione di una dipendenza lineare dal potenziale di membrana per
la corrente ionica complessiva. Il processo di adattamento della frequenza di emissione degli impulsi può essere incluso nel modello LIF aggiungendo all’equazione
fondamentale un’ulteriore termine di corrente Ia = −rm gsra(V − EK ),
τm
dV
= EL − V − rm gsra (V − EK ) + Rm Ie .
dt
(2.11)
La conduttanza associata all’adattamento della frequenza di emissione degli impulsi
gsra è stata schematizzata come una conduttanza K + , cosicché, quando viene attivata, iperpolarizza il neurone, rallentando qualsiasi impulso che può sopraggiungere.
EK è il potenziale di inversione del potassio. Assumiamo che questa conduttanza si rilassi esponenzialmente a 0 con una costante temporale τsra soddisfacendo
l’equazione
τsra
dgsra
= −gsra .
dt
(2.12)
Ogniqualvolta un neurone genera un impulso, gsra è accresciuto di un fattore ∆gsra ,
cioè gsra → gsra + ∆gsra ; durante una sequenza di potenziali d’azione emessi, la
corrente si modifica attraverso una sequenza di passi successivi che causano una
diminuzione della frequenza di emissione (come mostrato in figura 2.6).
La probabilità che un neurone spari è significativamente ridotta nel breve lasso temporale successivo alla generazione di un potenziale di azione; tale effetto di
refrattarietà non è incluso nel modello base LIF. Il modo più semplice per introdurre nel modello un periodo di refrattarietà assoluto è quello di aggiungere una
condizione alla regola base di superamento della soglia tale che proibisca l’emissione
di un altro potenziale di azione per un periodo di tempo immediatamente successivo
all’emissione dell’impulso. La refrattarietà può essere incorporata in un modo più
realistico aggiungendo una conduttanza simile a quella introdotta per l’adattamento in frequenza di emissione dei potenziali di azione; stavolta però la conduttanza
dovrà avere un tempo di recupero più veloce ed un incremento più grande in seguito all’emissione di un potenziale di azione. Grazie ad un consistente incremento,
dovuto all’emissione di un potenziale di azione, il valore del potenziale del neurone
si avvicina al potenziale di equilibrio del potassio EK , prevenendo in maniera temporanea un ulteriore sparo e producendo un periodo di refrattarietà assoluto. Nel
momento in cui questa conduttanza si avvicina a zero, l’emissione del potenziale
di azione sarà nuovamente possibile anche se inizialmente poco probabile. Questo
meccanismo produce cosı̀ anche un periodo di refrattarietà relativo.
Capitolo 3
Modelli di reti neurali ad
accoppiamento impulsivo
I singoli neuroni, di svariate tipologie e morfologie, sono connessi in reti assai complesse tramite sinapsi chimiche ed elettriche nelle varie aree del cervello, presenti in
tutti i vertebrati e in molti invertebrati. Ad esempio, il cervello umano contiene circa
100 miliardi di neuroni ed ogni neurone può essere connesso ad un gran numero di
altri neuroni, sino a 10 mila. La complessità della rete cerebrale è tale da non poter
essere studiata in modo numerico (o teorico) con un approccio diretto, cioè realizzando una riproduzione il più fedele possibile del cervello o di porzioni di esso, questo sia
perché entrare in dettagli estremi di descrizione della rete neurale rischia, a causa
della presenza di un numero elevatissimo di parametri da calibrare, di rendere lo
stato della rete sensibilissimo a piccole variazioni dei parametri stessi, sia perché da
un punto di vista numerico, la simulazione di questa rete diverrebbe assai onerosa
in termini di calcolo, rendendo possibili solo simulazioni per brevissimi intervalli
temporali. Per lo studio della dinamica di reti neurali è allora necessario ricorrere a
modelli mesoscopici, che si possono ottenere con vari livelli di approssimazione. In
questo e nel prossimo capitolo ci occuperemo di reti di neuroni leaky integrate-andfire ad accoppiamento impulsivo, sia globalmente connesse, che con diluizione nella
connettività. Nonostante l’estrema semplicità dei modelli di rete considerate, queste
danno luogo a dinamiche collettive assolutamente non banali. Nel primo paragrafo
introdurremo un modello di rete leaky integrate-and-fire globalmente accoppiata;
ridurremo le equazioni differenziali che ne descrivono la dinamica ad una mappa a
tempo discreto ed introdurremo l’analisi di stabilità lineare relativa ai modelli in
questione. Nel secondo paragrafo effettueremo l’analisi di stabilità di stati collettivi
della rete, distinguendo tra i modi di lunghezze d’onda grandi e quelli di lunghezze
d’onda brevi. Infine nell’ultimo paragrafo considereremo una rete diluita ed analizzeremo gli effetti che tale diluizione comporta, come l’osservazione, in regime di
caos stabile, di transitori che divergono esponenzialmente con il numero di neuroni
della rete. .
3.1
Reti neurali con accoppiamento impulsivo
Una rete neurale è, formalmente, un grafo i cui nodi sono costituiti dai neuroni e
le cui connessioni rappresentano le sinapsi; in particolare, ciascuna connessione è
pesata con la corrispondente efficienza sinaptica [8]. Le sinapsi costituiscono cosı̀ un
grafo con connessioni unidirezionali ed orientate. Ciascun nodo è caratterizzato da
un’equazione di evoluzione in cui lo stato del neurone dipende dai neuroni connessi
ad esso, ovvero dai neuroni presinaptici; i pesi sinaptici possono essere fissati oppure
possono anche evolvere nel tempo (plasticità sinaptica), in accordo con la storia dei
due nodi connessi dalla sinapsi [9, 20]. Se consideriamo le reti neurali come sistemi
dinamici, possiamo dare una formulazione canonica della dinamica neurale; ciascun
neurone i è caratterizzato dal suo stato, xi , che appartiene ad un certo insieme
compatto Ξ ∈ Rq , dove q è il numero di variabili che caratterizzano lo stato di un
neurone. Assumiamo inoltre che tutti i neuroni siano descritti dallo stesso numero di
variabili. Il LIF corrisponde al caso in cui q = 1, xi = Vi è il potenziale di membrana
del neuroni i e Ξ = [R,Θ], come mostrato nel paragrafo (2.2). L’evoluzione di N
neuroni è data cosı̀ da un sistema dinamico deterministico del tipo:
dx
= Fγ (x,t),
dt
tempo continuo,
(3.1)
o,
x(t + 1) = fγ [x(t),t],
tempo discreto.
(3.2)
La variabile x = {xi }N
i=1 rappresenta lo stato dinamico di una rete con N neuroni
al tempo t; tipicamente x ∈ M = Ξ N , dove M è lo spazio delle fasi dell’equazione
(3.2) ed Fγ (M) ⊂ M. La funzione Fγ : M → M dipende da un insieme di
parametri γ ∈ Rp ; il caso tipicamente considerato in seguito sarà γ = (Gc , I(ext) ),
dove Gc è la matrice N × N dei pesi sinaptici, mentre I(ext) rappresenta il vettore
N-dimensionale delle correnti o stimoli esterni ricevuti dai singoli neuroni. Cosı̀ γ
è un punto nello spazio dei parametri di controllo di dimensione p = N 2 + N.
Un neurone i emette un potenziale d’azione ogni qual volta il suo stato xi appartiene ad una certa regione connessa P1 del suo spazio delle fasi, altrimenti è quiescente se x ∈ P0 = Ξ\P1 . Per N neuroni identici questo porta ad una “partizione
naturale” P dello spazio delle fasi M. Chiamiamo Γ = {0,1}N , ω = [ωi ]N
i=1 ∈ Γ ,
allora P = {Pω }ω∈Γ , dove Pω = Pω1 ×Pω2 × · · · × PωN . Equivalentemente, se
x ∈ Pω , si ha che tutti i neuroni con ωi = 1 stanno emettendo impulsi, mentre
quelli con ωk = 0 sono quiescenti.
A ciascuna condizione iniziale x ∈ M possiamo associare un “raster plot” definito come ω̃ ≡ {ω(t)}+∞
t=0 tale che x(t) ∈ Pω (t) , ∀t ≥ 0; cosı̀ ω̃ è la sequenza di
configurazioni successive dei neuroni della rete che emettono impulsi quando viene
preparata nella condizione iniziale x (vedi figura 3.1). Il “raster plot” è la successione dei tempi di emissione dei potenziali di azione di tutti i neuroni della rete
100
0.8
80
Indice di Neurone
1
0.6
vk
0.4
0.2
60
40
20
(a)
0
226
226.2
226.4
226.6
Tempo
226.8
227
227.2
(b)
0
1750
1800
1850
1900
1950
Tempo
Figura 3.1. (a) La figura mostra l’andamento del potenziale di membrana del kesimo neurone in funzione del tempo, in una rete omogenea di N neuroni. (b) Nella
seconda figura è riportato l’indice del neurone che emette un impulso in funzione
del tempo, una volta che gli indici dei neuroni sono stati inizialmente ordinati.
Questo “raster plot” corrisponde ad uno stato asincrono. [10]
che partecipano alla dinamica soprasoglia. Ad esempio, supponiamo di aver a che
fare con una rete omogenea di N neuroni. In questo caso l’ordine con cui i vari
neuroni emettono in sequenza potenziali d’azione non cambia nel tempo [11]; allora
nel caso dello stato asincrono (o ”splay state” di cui parleremo nel paragrafo 3.1.1),
caratterizzato da una frequenza di sparo costante T /N, ove T è l’ISI uguale per ogni
neurone, il raster plot assume il semplice aspetto riportato in figura (3.1)
3.1.1
Modello di rete di neuroni LIF globalmente accoppiati
La comprensione di alcuni aspetti dei meccanismi di elaborazione dell’informazione
nel cervello può essere perseguita analizzando le proprietà dinamiche dei modelli di
reti neurali; pensare di avvicinarsi a questo problema nella sua assoluta generalità
è un obiettivo incredibilmente ambizioso, dal momento che occorre tenere in conto
(i) del ruolo della topologia delle connessioni, (ii) della dinamica delle stesse connessioni, al fine di rappresentare la plasticità sinaptica, (iii) della dinamica interna a
ciascun modello di neurone, che può dipendere dal numero di canali ionici ma anche
da altre variabili e parametri, (iv) dalla diversità tra i neuroni e le loro connessioni e,
infine, (v) dall’inevitabile presenza di rumore. Ad ogni modo possiamo congetturare
che almeno alcuni meccanismi di base siano robusti e possano dipendere solo da
pochi ingredienti; infatti anche i modelli semplici composti da unità identiche globalmente accoppiate esibiscono proprietà dinamiche interessanti e, indubbiamente,
non ovvie e non totalmente comprese. Consideriamo ad esempio il cosidetto “splay
state” (o stato asincrono), che costituisce un modo collettivo che emerge in reti di
oscillatori non lineari completamente accoppiati (vedi figura 3.1) [5]; questo stato è
caratterizzato dal fatto che tutte le oscillazioni abbiano la stessa forma d’onda X e
che le fasi di tali oscillatori si dispongano sul cerchio unitario nel piano complesso
in modo equispaziato. In questo caso lo stato del singolo oscillatore xk può essere
descritto al tempo t da
xk (t) = X(t + kT /N) = A cos(ωt + 2πk/N);
ω = 2π/T ;
k = 1, · · · ,N
(3.3)
dove N è il numero di oscillatori del sistema, T il periodo dell’oscillazione collettiva,
X la forma d’onda comune, 2πk/N è la fase di ogni oscillatore ed A l’ampiezza
dell’oscillazione stessa. La stabilità degli stati stazionari di questi sistemi è ancora
un problema dibattuto [5, 12].
Il metodo usato di solito per determinare le proprietà di stabilità di tali semplici modelli è basato sull’approssimazione di campo medio [5]; questo ci permette
di ottenere lo spettro degli autovalori associati alla matrice di stabilità nel limite termodinamico N → ∞, dove N denota il numero di neuroni. La stima della
stabilità lineare dello stato asincrono costituisce il passo preliminare verso una completa comprensione delle proprietà dinamiche della rete neurale; per effettuare tale
stima si può introdurre la sezione di Poincaré, (vedi appendice B), che trasforma il
sistema dinamico originale in una mappa che connette le configurazioni dinamiche
della rete neurale corrispondenti a istanti successivi in cui si ha l’emissione di impulsi
consecutivi da parte di un neurone qualsiasi della rete come vedremo nei paragrafi
successivi.
Consideriamo dunque una rete di N neuroni identici LIF; la dinamica dell’iesimo neurone è descritta da una singola variabile, il potenziale di membrana vi (t),
che obbedisce all’equazione differenziale
v̇i = a − vi + gE(t),
i = 1, · · · ,N,
(3.4)
dove tutte le variabili e i parametri sono espressi in unità adimensionali opportunamente riscalate (vedi paragrafo 2.2.1). In accordo con la precedente equazione,
in assenza del campo esterno E(t) e per a > 1, il potenziale di membrana rilassa
al valore a, ma, non appena raggiunge il valore di soglia vi = 1, viene riscalato a
vi = 0 e viene inviato, simultaneamente, un impulso a tutti gli altri neuroni (questa
procedura di riassegnazione del valore del potenziale è un modo approssimato per
descrivere il meccanismo di scarica presente nei neuroni reali). Come già ricordato
nel paragrafo (2.2.1) il parametro a > 1 corrisponde alla corrente di ingresso soprasoglia, mentre g regola l’ampiezza del campo E(t) agendo come accoppiamento
efficace. Il campo E(t) è la sovrapposizione lineare degli impulsi emessi nel passato
ogniqualvolta il potenziale di membrana di ciascun singolo neurone raggiunge il valore di soglia. Assumendo che la forma di ogni impulso sia data da Es (t) =
α2 t −αt
e
N
,
dove 1/α è la larghezza temporale dell’impulso [5], allora l’evoluzione del campo
totale è data dall’equazione [5]:
Ë(t) + 2αĖ(t) + α2 E(t) =
α2 X
δ(t − tn ) ,
N n|tn <t
(3.5)
dove la sommatoria nel membro a destra rappresenta il termine di sorgente dovuto
agli impulsi emessi a tempi tn < t. Quindi la dinamica della rete è data da N
equazioni differenziali ordinarie del primo ordine del tipo (3.4) più la (3.5) che è
un’equazione del secondo ordine e descrive l’evoluzione del campo. In totale si
hanno quindi N + 2 gradi di libertà.
3.1.2
Mappa guidata dall’evento
È conveniente trasformare le equazioni differenziali in una mappa a tempo discreto;
per fare questo occorre integrare l’equazione (3.5) tra il tempo tn e il tempo tn+1 ,
dove tn è il tempo immediatamente successivo all’emissione dell’n-simo impulso. La
mappa risultante associata alla dinamica del campo macroscopico E è
E(n + 1) = E(n)e−ατ (n) + NQ(n)τ (n)e−ατ (n)
Q(n + 1) = Q(n)e−ατ (n) +
α2
,
N2
(3.6)
(3.7)
dove τ (n) = tn+1 − tn è l’intervallo temporale tra un impulso e il successivo e
dove abbiamo introdotto la nuova variabile Q := (αE + Ė)/N. L’equazione (3.4)
può essere integrata esplicitando la dipendenza temporale nota del campo E fra un
impulso e l’altro,
vi (n + 1) = vi (n)e−τ (n) + a 1 − e−τ (n) + gF (n)
i = 1, . . . ,N .
(3.8)
dove F è
e−τ (n) − e−ατ (n)
NQ(n)
τ (n)e−ατ (n)
F (n) =
E(n) +
−
NQ(n) .
α−1
α−1
(α − 1)
!
(3.9)
L’intervallo temporale tra un impulso e il successivo τ è ottenuto imponendo la
condizione vm (n + 1) = 1,
"
vm (n) − a
τ (n) = ln
1 − gF (n) − a
#
.
(3.10)
dove l’indice m identifica il neurone più vicino a soglia al tempo τ . Le equazioni
(3.8) e (3.9) possono essere scritte in una forma più compatta esprimendo F (n) come
funzione di τ (n) per mezzo dell’equazione (3.10), cioè
vi (n + 1) = vi (n)e−τ (n) + 1 − vm (n)e−τ (n)
j = 1, . . . ,N − 1 .
(3.11)
Dal momento che in una rete di neuroni indistinguibili globalmente accoppiati viene
preservato l’ordine dei potenziali vi [11], è conveniente per prima cosa ordinarli e
poi mettersi in un sistema di riferimento solidale con uno qualsiasi dei neuroni;
si ha perciò la trasformazione di variabili xj (n) = vj−n (n). In questo sistema di
riferimento l’indice del neurone più vicino a soglia è sempre lo stesso e può essere
scelto uguale a 1, senza perdere in generalità; l’equazione di evoluzione può dunque
essere riscritta come
xj−1 (n + 1) = xj (n)e−τ (n) + 1 − x1 (n)e−τ (n)
j = 1, . . . ,N − 1 ,
(3.12)
con la condizione al contorno xN = 0 e dove,
"
x1 (n) − a
τ (n) = ln
1 − gF (n) − a
#
.
(3.13)
L’insieme di equazioni (3.6, 3.7, 3.12, 3.13, 3.9) definisce una mappa a tempo
discreto che è completamente equivalente all’insieme di equazioni differenziali di
partenza. Si ottiene cosı̀ che una rete di N neuroni identici può essere descritta
per mezzo di N + 1 equazioni, due delle quali tengono conto della dinamica del
campo macroscopico, mentre le rimanenti N − 1 equazioni descrivono l’evoluzione
dei neuroni. Un grado di libertà è stato perso a causa della sezione di Poincaré
effettuata (ovvero xN non è più una variabile dal momento che è stata posta, per
definizione, sempre uguale a 0). Inoltre, in questo sistema di riferimento, lo stato
asincrono periodico si riduce ad un punto fisso che soddisfa le seguenti condizioni:
τ (n) ≡
T
,
N
E(n) ≡ Ẽ ,
(3.14)
Q(n) ≡ Q̃ ,
x̃j−1 = x̃j e−T /N + 1 − x̃1 e−T /N ,
(3.15)
(3.16)
dove T è il tempo che intercorre tra due emissioni di impulso consecutive dello stesso
neurone. Attraverso un semplice calcolo si ottiene
Q̃ =
−1
α2 −αT /N −1
αT /N
1
−
e
,
Ẽ
=
T
Q̃
e
−
1
.
N2
La soluzione dell’equazione (3.16) coinvolge una serie geometrica, la quale, insieme
alla condizione al contorno x̃N = 0, porta ad un’equazione trascendente per il periodo T . Per semplicità riportiamo la soluzione esplicita contenente solo i termini
all’ordine O(1/N) nel limite N ≫ 1,
aT + g 1 − e−j T /N ,
"T
#
aT + g
T = ln
.
(a − 1)T + g
x̃N −j =
(3.17)
(3.18)
Se supponiamo di aver a che fare con neuroni soprasoglia, cioè se prendiamo a > 1,
il periodo T è ben definito nel caso eccitatorio (g > 0) solo per g < 1 (T → 0
quando g si avvicina ad 1), mentre nel caso inibitorio (g < 0), esiste una soluzione
significativa per qualsiasi valore dell’accoppiamento (inoltre T → ∞ per g → −∞).
3.1.3
Analisi di stabilità lineare
Al fine di effettuare l’analisi di stabilità dello stato asincrono, è necessario linearizzare le equazioni (3.6, 3.7, 3.12) attorno al punto fisso (3.14, 3.15, 3.16), cioè:
δE(n + 1) = e−αT /N δE(n) + T e−αT /N δQ(n)
−
(3.19)
αẼ − N Q̃e−αT /N δτ (n) ,
δQ(n + 1) = e−αT /N δQ(n) − αQ̃e−αT /N δτ (n) ,
δxj−1 (n + 1) = e−T /N [δxj (n) − δx1 (n)] + e−T /N (x̃1 − x̃j )δτ (n) ,
(3.20)
(3.21)
dove δE, δQ, {δx} rappresentano le perturbazioni lineari delle variabili corrispondenti e dove abbiamo introdotto per sinteticità δτ (n), la cui espressione può essere
ottenuta linearizzando le equazioni (3.9, 3.13)
δτ (n) = τx δx1 (n) + τE δE(n) + τQ δQ(n) ,
con τx := ∂τ /∂x1 , τE := ∂τ /∂E e τQ := ∂τ /∂Q.
(3.22)
1.0
Im{µk}
0.5
0.0
-0.5
-1.0
-1.0
-0.5
0.0
Re{µκ}
0.5
1.0
Figura 3.2. Cerchio unitario e spettro dei moltiplicatori di Floquet per la mappa
completa per N = 20 (cerchi rossi) e N = 10 (cerchi blue) per accoppiamento
eccitatorio. I parametri sono a = 3.0, g = 0.4, e α = 30.0.[10]
La condizione al contorno xN ≡ 0 dovuta al sistema di riferimento mobile impone
che δxN = 0. In pratica, il problema di stabilità è risolto calcolando lo spettro
dei moltiplicatori di Floquet1 {µk }, k = 1, · · · ,N + 1, associati con il problema agli
autovalori dell’insieme di equazioni lineari (3.19, 3.20, 3.21); tale calcolo deve essere,
in generale, effettuato, numericamente. Discutiamo innanzitutto il caso banale g =
0; in questo caso si trova che µk = exp(iϕk ), dove ϕk =
2πk
,
N
k = 1, · · · ,N − 1, e
µN = µN +1 = exp(−αT /N). Gli ultimi due esponenti interessano la dinamica del
campo E(t), il cui decadimento è regolato dalla scala temporale α−1 . Non appena
l’accoppiamento g > 0, piccole fluttuazioni di ampiezza ∼ O(g/N) influenzano la
dinamica dei neuroni e i moltiplicatori dello spettro di Floquet assumono la forma
generica
µk = eiϕk eT (γk +iωk )/N , ϕk =
2πk
, k = 1, . . . ,N − 1 ,
N
(3.23)
µN = eT (γN +iωN )/N , µN +1 = eT (γN+1 +iωN+1 )/N ,
dove γk e ωk sono la parte reale e immaginaria degli esponenti di Floquet.
In figura (3.2) mostriamo lo spettro dei moltiplicatori di Floquet dello stato asincrono nel caso di accoppiamento eccitatorio e valori di N finiti. I moltiplicatori con
1
La teoria generale dell’analisi di stabilità per mezzo dello spettro dei moltiplicatori di Floquet
sarà discussa in dettaglio in appendice C.1.
k = 1, · · · ,N − 1 sono molto vicini al cerchio unitario, mentre i due moltiplicatori
isolati µN e µN +1 giacciono molto vicini all’asse reale all’interno del cerchio unitario.
Dal momento che, già per g/N ≈ O(10−2 ), i moltiplicatori del caso accoppiato possono essere visti come una piccola “perturbazione” del caso non accoppiato (cioè
con g = 0), possiamo cercare di dar vita ad un approccio perturbativo. Prima di effettuare questo tipo di analisi occorre sottolineare che la variabile ϕk gioca un ruolo
analogo a quello del numero d’onda nell’analisi di stabilità lineare di sistemi spazialmente estesi, cosı̀ che possiamo dire che γk caratterizza la stabilità del k-esimo modo.
Nell’analisi che segue è conveniente distinguere tra i modi caratterizzati da ϕk ≈ 0,
mod(2π) +O(1/N) e tutti gli altri modi. Si identificano dunque due componenti
spettrali che richiedono di essere trattate in modo matematicamente diverso: la prima componente corrisponde alla condizione kµk − 1k ∼ N −1 ed è identificata con
la dicitura “lunghezze d’onda grandi” (LOG); la seconda componente corrisponde a
kµk − 1k ∼ O(1) ed è identificata con “lunghezze d’onda brevi” (LOB) [10].
3.2
Impulsi di durata finita
Analizziamo adesso il problema di stabilità dello stato asincrono per reti soggette
ad impulsi con α finito per grandi valori di N. Considerando i termini all’ordine
1/N, la mappa ad evento guidato (vedi equazioni (3.6, 3.7, 3.12) ) si semplifica nel
seguente insieme di N + 1 equazioni:
E(n + 1) = (1 − ατ )E(n) + NQ(n)τ ,
(3.24)
Q(n + 1) = (1 − ατ )Q(n) +
(3.25)
α2
,
N2
xj−1 (n + 1) = (1 − τ )xj (n) + 1 − x1 (n) + τ ,
(3.26)
dove j = 1, . . . ,N −1 mentre τ x1 è stato approssimato con τ poiché 1−x1 ≈ O(1/N).
L’espressione per l’intervallo tra una emissione e la successiva del potenziale di azione
(3.13) si semplifica cosı̀ in
τ (n) =
1 − x1 (n)
.
a − 1 + gE(n)
(3.27)
La soluzione periodica per il campo che tiene conto di tutti gli impulsi diventa
Ẽ = T −1 e Q̃ = α/NT , mentre x̃j e il periodo T sono ancora dati dall’equazioni
(3.17, 3.18). Lo spettro degli autovalori di Floquet µk , k = 1, · · · ,N + 1 può essere
ottenuto linearizzando le equazioni (3.24, 3.25, 3.26) nell’intorno di questa soluzione
periodica e assumendo che ciascuna perturbazione cresca come µk
δE(n + 1) = µk δE(n) = (1 − αT /N)δE(n) + T δQ(n) ,
(3.28)
δQ(n + 1) = µk δQ(n) = (1 − αT /N)δQ(n) −
(3.29)
α2
δτ (n) ,
NT
δxj−1 = µk δxj−1 (n) = (1 − T /N)δxj (n) − δx1 (n) + (1 − x̃j )δτ (n) , (3.30)
Un’espressione esplicita per δτ si può ottenere valutando la derivata dell’equazione
(3.27)
δτ = −
T2
T
δE − δx1 .
N
g
Sostituendo quanto trovato nelle equazioni (3.28, 3.29, 3.30), vediamo che il problema agli autovalori consiste nel trovare le N +1 radici µk del polinomio associato; una
semplificazione parziale del problema può essere ottenuta estraendo dalle equazioni
(3.29) e (3.30) la dipendenza di δτ dalla perturbazione del potenziale del neurone
più vicino a soglia δx1
δτ = Kδx1
(3.31)
dove
α2 gT
K = −(a − 1 + g/T ) + 2
N (µk − 1 + αT /N)2
"
#−1
.
(3.32)
Infine, sostituendo questa espressione nell’equazione (3.30), otteniamo un insieme
chiuso di equazioni per le perturbazioni del potenziale di membrana,
µk δxj−1 = (1 − T /N)δxj + (K − 1)δx1 − K x̃j δx1 .
(3.33)
Dopo aver imposto la condizione al contorno δxN = 0, l’equazione (3.33) si riduce
alla seguente equazione implicita agli autovalori:
µkN −1 eT = K(a + g/T )
1 − µkN −1
1 − µkN −1 eT
− [K(a − 1 + g/T ) + 1]
,
1 − µk
1 − µk eT /N
(3.34)
dove K è una funzione di µk ed è dato dall’equazione (3.32). Al fine di risolvere
questa equazione analiticamente è necessario effettuare la distinzione tra lunghezze
d’onda grandi e piccole.
3.2.1
Lunghezze d’onda grandi
Innanzitutto consideriamo i modi per cui kµk − 1k ∼ N −1 (o, equivalentemente,
ϕk ≈ 0, mod(2π) +O(1/N)). Al fine di semplificare la notazione definiamo
Λk :=
N
ln µk = γk + iωk ,
T
con ϕk ≈ 0, mod(2π).
All’ordine principale O(1/N), K vale
α2 g
K = −(a − 1 + g/T ) +
T (Λk + α)2
"
#−1
.
Sostituendo questa espressione nell’equazione agli autovalori (3.34) e rimuovendo i
termini di ordine 1/N, si ottiene
aT + g 2
T
−Λk T
−Λk T
, ||Λk || =
6 0.
(Λ
+
α)
(Λ
+
1)
=
Λ
e
−
e
1
−
e
k
k
k
α2 g
(3.35)
Questa equazione coincide con l’approssimazione derivata da Abbott e van Vreeswijk
[5] (che nel presente contesto corrisponde ad effettuare un “limite del continuo”,
ovvero a considerare solo lunghezze d’onda grandi), eccetto per il fattore ||Λk || = 0,
che corrisponde all’esponente di Floquet zero dell’evoluzione temporale continua
(3.4) e che scompare nella dinamica a tempo discreto. Occorre sottolineare ancora
che, nonostante l’equazione (3.35) abbia N + 1 radici, questa dà una soddisfacente
approssimazione solo per quegli autovalori che soddisfano la relazione ||µk − 1|| ∼
N −1 , cioè per quegli autovalori che giacciono vicino al punto (1,0) (vedi figura 3.2).
3.2.2
Lunghezze d’onda brevi
La seconda componente dello spettro (3.23) è ottenuta quando ||µk − 1|| ∼ O(1). In
questo caso l’espressione (3.32) si semplifica alquanto,
K = −(a − 1 + g/T )−1 .
Introducendo nell’equazione (3.34) la forma esplicita della soluzione periodica (3.18),
si ottiene una notevole semplificazione anche per lo spettro, ovvero
−T
µN
k = e
a + g/T
=1.
a − 1 + g/T
(3.36)
Questo risultato ci dice che abbiamo uno spettro di Floquet completamente degenere,
ωk ≡ 0 , γ k ≡ 0
(3.37)
Ricordiamo che questa approssimazione vale solo per quegli autovalori per cui ||µk −
1|| ∼ O(1), ovvero vale per la maggior parte dello spettro, eccetto quegli autovalori
che giacciono vicino al punto (1,0), dove il cerchio unitario intercetta l’asse reale
(vedi fig. 3.2). Inoltre il risultato (3.37) è esatto nel limite N → ∞, mentre il caso
ad N finito verrà trattato nel paragrafo successivo.
Per quanto riguarda gli autovalori isolati µN e µN +1 , si può facilmente intuire
che questi possano essere sempre contenuti all’interno del cerchio unitario, vicino
all’asse reale, per N finiti e ampiezze dell’impulso finite, e che si avvicinino al punto
(1,0) da sinistra nel limite N → ∞; dunque questi possono al più contribuire alla
stabilità marginale della dinamica complessiva.
3.2.3
Diagramma di fase e correzioni di taglia finita
In accordo con i precedenti risultati possiamo dire che, nel limite N → ∞, il manifestarsi dell’instabilità è determinato dagli esponenti di Floquet associati con le
LOG, dato che lo spettro associato alle LOB (3.37) è esattamente nullo. Inoltre si
α
200
150
INSTABILE
100
50
STABILE
0
0
0.2
0.4
g
0.6
0.8
1
Figura 3.3. Diagramma di fase per la stabilità lineare dello stato asincrono in una
rete neurale con accoppiamento eccitatorio mediata da impulsi di durata finita. La
linea continua che separa la regione stabile da quella instabile nel piano (g,α) è
stata ricavata dalla formula analitica dello spettro di Floquet (3.35) con a = 1.3 .
Occorre sottolineare che, in questo contesto, stabile si riferisce ad N finiti, dal
momento che per sistemi infiniti la stabilità diventerà marginale.[10]
ottiene che lo stato asincrono è sempre instabile per accoppiamento di tipo inibitorio
(g < 0). Nel caso di accoppiamento eccitatorio l’analisi di Abbott e van Vreeswijk
[5] predice stabilità per lo stato asincrono per α ≤ αc (g,a), dove αc (g,a) è la linea
critica che separa la regione stabile da quella instabile (vedi figura 3.3). Questa
linea corrisponde ad una biforcazione di Hopf sovracritica che dà vita ad un nuovo
comportamento periodico collettivo chiamato sincronizzazione parziale (vedi paragrafo 3.2.4). Inoltre si ha che αc diverge a +∞ per g → 1 (mentre per g > 1 non
può essere sostenuto un regime stazionario dal momento che l’evoluzione accelera in
maniera uniforme). Nel limite opposto di accoppiamento che si annulla (g → 0), la
biforcazione sopravvive; dall’equazione (3.35) si può vedere inoltre che la frequenza
ωc della soluzione di biforcazione converge a ωc = 2π/T e αc = −1 +
q
1 + ωc2 .
Includendo il ruolo dei modi con LOB possiamo concludere che, nel limite N →
∞, lo stato stazionario può essere al più marginalmente stabile per α ≤ αc (g,a).
Nel caso di numero di neuroni finito si verifica, risolvendo numericamente le equazioni
(3.19, 3.20, 3.21), che lo stato asincrono risulta strettamente stabile e che l’esponente
di Floquet massimo tende a zero da valori negativi con un andamento del tipo 1/N 2
10
-2
γk
(a)
|γk|
0
(b)
-0.001
10
-3
-0.002
10
10
-4
-0.003
-0.004
-5
-0.005
10
-6
10
0
10
1
10
2
k
10
3
-600 -400 -200
0
ϕkN
200
400
600
Figura 3.4. (a) Grafico in scala doppiamente logaritmica dei valori assoluti degli
esponenti di Floquet γk , ordinati dal più grande al più piccolo come funzione
dell’indice k = 1,...,N per N = 100,200,400. La linea tratteggiata ha una pendenza
di -2. (b) Esponente di Floquet come funzione della fase riscalata ϕN , per N = 100
(cerchi neri) e N = 200 (cerchi rossi). In entrambe le figure i valori dei parametri
sono a = 3.0, g = 0.4, e α = 30.0.[10]
(vedi figura 3.4) [5].
Questo implica che una soluzione approssimata all’ordine 1/N della mappa ad
evento guidato non può tener conto delle instabilità del modello originale, che sono
dell’ordine 1/N 2 . Questo è confermato dalla figura (3.5) dove gli spettri di Floquet ottenuti con approssimazioni al primo e al secondo ordine della mappa guidata
dall’evento danno luogo ad uno stato asincrono instabile, anche se la soluzione numerica del problema di stabilità del modello esatto indica che il modello ad N finito
è stabile. Quindi nello studio di questi sistemi va fatta estrema attenzione al livello
di approssimazione usato.
Riassumendo, la stabilità dello stato asincrono può essere indagata riducendo un
modello di equazioni differenziali globalmente accoppiate a delle opportune mappe
guidate dall’evento, che mettono in relazione le configurazioni della rete corrispondenti a due emissioni consecutive di potenziali di azione. L’analisi analitica dello
Jacobiano nel limite di grandi N rivela che lo spettro degli autovalori è costituito
da due componenti: (i) modi propri di grandi lunghezze d’onda; (ii) modi propri di
brevi lunghezze d’onda. Un approccio di campo medio (o di “limite del continuo”)
è capace di riprodurre la parte dello spettro associata ai modi di grandi lunghezze
8×10
-4
γk
4×10
-4
0
-4×10
-4
-4
-8×10 -π
-π/2
0
π/2
ϕk
π
Figura 3.5. Esponenti di Floquet γk (ϕ) come funzione della fase ϕk per impulsi
di durata finita α = 30.0 e numero di neuroni finito N = 500 nel caso di accoppiamento eccitatorio g = 0.4. I cerchi pieni neri rappresentano il risultato esatto
per N finito, mentre i quadrati rossi vuoti e i triangoli blu vuoti si riferiscono a
risultati approssimati, corretti rispettivamente fino al primo e al secondo ordine in
1/N . Il parametro qui è a = 3.[10]
d’onda col rischio però di non catturare eventuali instabilità che si manifestassero a
lunghezze d’onda piccole.
3.2.4
Altri stati collettivi della rete
Discutiamo brevemente adesso le caratteristiche della soluzione collettiva che nasce
al di sopra della linea αc (g,a) (vedi figura 3.3), detta stato di sincronizzazione
parziale. In questo regime il campo E(t) esibisce una dinamica periodica che si manifesta in assenza di qualsiasi sincronizzazione tra i singoli neuroni, i quali mostrano
invece un moto quasi periodico, cioè caratterizzato da due frequenze non commensurabili fra loro [6, 29]. La sincronizzazione parziale deriva dalla destabilizzazione
dello stato asincrono, che è invece caratterizzato da un campo medio costante e da
un comportamento periodico dei singoli neuroni, con fasi equispaziate.
In una rete di neuroni LIF, in cui l’accoppiamento impulsivo è modellizzato da
una funzione α, come in (3.5), troviamo che, per accoppiamenti eccitatori, le reti
evolvono verso uno stato asincrono se α è piccolo, cioè per impulsi di lunga durata.
Quando α aumenta, la rete inizia a sincronizzarsi; per costanti di tempo finite la
3
2.5
2
E
1.5
1
0.5
0
356
357
358
359
360
Tempo
Figura 3.6. Andamento del campo E in funzione del tempo nel regime di sincronizzazione parziale e in assenza di rumore additivo. La simulazione è stata
effettuata utilizzando i seguenti valori dei parametri: α = 9, g = 0.4, a = 1.3. In
questo caso αc = 8.34 ± 0.01 [29].
rete non raggiunge sincronia completa anche se è costituita da oscillatori identici e
il sistema è completamente privo di rumore. Solo nel limite di α → ∞ (cioè per
durate dell’impulso che tendono a zero), lo stato diventa completamente sincronizzato [29]. Dunque se percorriamo il diagramma di fase nel piano (g,α) mantenendo
l’accoppiamento g costante, passiamo, al crescere di α, dallo stato asincrono alla
sincronizzazione parziale e solo nel limite α → ∞ otteniamo una sicronizzazione
completa.
Con accoppiamento inibitorio la rete sincronizza completamente per α piccoli; al
crescere di α la rete si divide in due o più gruppi di neuroni completamente sincronizzati al loro interno. Il numero medio di questi gruppi cresce al crescere di α, sebbene
il numero esatto di tali gruppi dipenda dalle condizioni iniziali. Per una rete con un
numero grande ma finito di oscillatori il numero di gruppi che si formano tenderà
ad essere pari al numero di neuroni, dunque, lo stato finale sarà indistinguibile dallo
stato asincrono. Cosı̀ con accoppiamento inibitorio, il sistema passa da uno stato
completamente sincronizzato per piccoli α, ad uno stato sostanzialmente asincrono
per grandi α, attraverso la formazione di un numero crescente di raggruppamenti di
neuroni completamente sincronizzati al loro interno.
Dato che il regime di sincronizzazione parziale sarà il soggetto principale del
lavoro originale di questa tesi descriviamo ora in maggior dettaglio la dinamica della
rete associata a tale stato collettivo. Come mostrato in figura (3.6) la dinamica del
campo è ora periodica, mentre, come già detto, nel caso dello stato asincrono era
costante. A questo si associa l’andamento periodico della frequenza istantanea di
emissione degli impulsi, definita come
π(t) =
1
N(tm+1 − tm )
,
(3.38)
dove (tm+1 − tm ) ≈ (1/N) è l’intervallo tra due spari consecutivi della rete. Il
membro a sinistra di questa equazione non presenta il pedice m, perché nel limite
N → ∞ la variabile temporale diventa continua. L’andamento periodico è mostrato
in figura (3.7c), mentre nel caso dello stato asincrono era costante.
Un’altra peculiarità dello stato di sincronizzazione parziale è il fatto che gli ISI
dei singoli neuroni differiscano dal periodo della dinamica macroscopica; in altre
parole i tempi tra un’emissione e la successiva di un impulso, da parte del singolo neurone, sono sempre più piccoli del periodo di oscillazione del campo forzante.
Possiamo spiegare il fenomeno, in maniera qualitativa, osservando che, da un lato, i neuroni tendono a raggrupparsi, dall’altro, i neuroni che si trovano sul fronte
del raggruppamento tendono a sfuggire al gruppo, mentre quelli che raggiungono il
gruppo dalle retrovie vi si uniscono. Questo giustifica anche il nome di “sincronizzazione parziale” attribuito a questo fenomeno. Dunque la dinamica quasi-periodica
dei singoli neuroni (vedi figura 3.7b) si combina in modo opportuno cosı̀ da generare una dinamica collettiva, espressa dal campo E(t), periodica. Questo si vede in
figura (3.7a), dove la curva chiusa riportata nel piano (E,Ė) rappresenta l’attrattore
associato alla dinamica collettiva della rete.
Infine, dalle analisi numeriche svolte sul modello originale soggetto a rumore
additivo, uniformemente distribuito e a media nulla, vediamo (figura 3.7(a)) che il
comportamento collettivo persiste, nonostante sia depresso dall’azione del rumore.
Il campo E ha un’ampiezza più piccola in presenza del rumore, mentre le fluttuazioni
sembrano descrescere all’aumentare del numero di oscillatori presenti nella rete con
√
un andamento del tipo 1/ N [6].
Figura 3.7. Risultati di simulazioni numeriche effettuate su una rete di N =
100 neuroni, utilizzando i seguenti valori dei parametri: α = 9, g = 0.4, a =
0.3. (a) Rappresentazione nel piano delle fasi (E,Ė). I punti corrispondono a
simulazioni effettuate in presenza di rumore additivo uniformemente distribuito; le
linee rappresentano invece le simulazioni effettuate in assenza di rumore additivo.
(b) Evoluzione, in funzione del tempo, dell’intervallo temporale tra uno sparo e
l’altro del singolo neurone (T ). (c) Evoluzione temporale della frequenza istantanea
π (B.1). [6]
3.3
Desincronizzazione in reti neurali diluite
In una rete corticale reale ogni neurone è connesso a moltissimi altri, ma non è
connesso a tutti i neuroni della corteccia cerebrale. È allora importante analizzare
l’effetto della diluizione del numero di connessioni fra i neuroni sulla dinamica di una
rete neurale. Per rete diluita si intende una rete in cui siano stati recisi dei legami fra
neuroni anche in modo asimmetrico. In particolare in questa sezione ci limiteremo
ad accoppiamenti solo inibitori, mentre il caso di accoppiamenti eccitatori sarà il
soggetto dei risultati originali della tesi (vedi cap.4).
Per comprendere il ruolo della diluizione, ricordiamo innanzitutto i risultati noti
per reti di neuroni LIF globalmente accoppiati. In quest’ambito sono di notevole
importanza i risultati rigorosi pubblicati da Jin in Ref. [11] per una rete non omogenea di neuroni LIF globalmente accoppiati, le cui connessioni siano prevalentemente
inibitorie. Jin ha dimostrato che, in questo modello, la sequenza di impulsi converge
a configurazioni periodiche stabili da quasi tutti gli stati iniziali. Ha dimostrato
inoltre che il tempo necessario a tale convergenza (detto transitorio) è finito ed al
massimo può divergere come una potenza del numero di neuroni nella rete nel limite
N → ∞; in particolare il transitorio si abbrevia al crescere dell’inibizione globale.
Si potrebbe osservare una divergenza del transitorio solo nell’eventualità che due
neuroni raggiungessero contemporaneamente la soglia, ma tale situazione si ottiene
solo per un insieme ristretto di stati iniziali dei neuroni, insieme che si restringe
sempre di più al crescere del livello di inibizione [11].
A partire dal modello di rete neurale con accoppiamento inibitorio, descritto in
[11], introduciamo la diluizione e mostriamo che nella versione diluita di tale modello
si possono osservare tipicamente dei transitori che crescono esponenzialmente con
il numero di neuroni nella rete, in presenza di un accoppiamento sufficientemente
grande, anche se l’esponente di Lyapunov2 massimo del sistema rimane negativo.
Questo fenomeno è noto in letteratura come “caos stabile” [30]. In altri termini, per
piccoli valori della costante di accoppiamento la dinamica converge, dopo un breve
transitorio, verso lo stato asincrono e l’unico effetto dovuto alla soppressione di una
piccola percentuale di legami tra i neuroni è la presenza di inomogeneità nelle mutue
interazioni che porta a piccole difformità negli intervalli tra un’emissione e l’altra
dell’impulso. D’altra parte, per valori dell’accoppiamento sufficientemente grandi,
sono osservati dei transitori che mostrano dinamica simil-stocastica, la cui durata è
esponenzialmente lunga con la dimensione della rete. Dal momento che vari indicatori mostrano che questo regime è stazionario, è logico aspettarsi che, nel limite
2
La caratterizzazione della dinamica in termini di esponenti di Lyapunov verrà discussa in
dettaglio in appendice C.2.
di reti infinitamente grandi, questo transitorio rappresenti una fase termodinamica
perfettamente legittima [12]. Dal momento che il caos stabile è dovuto alle discontinuità nell’evoluzione dinamica del sistema [30, 31], è naturale aspettarsi che questo
valga anche nel caso presente; osserviamo infatti che in presenza di disordine, dove
i neuroni non sono più l’uno equivalente all’altro, si verificano cambiamenti nella
sequenza con cui i neuroni emettono impulsi successivi e questa variazione di ordinamento induce discontinuità nell’evoluzione della rete. La transizione si manifesta
dunque come un fenomeno di desincronizzazione collettivo; tale fenomeno è analizzabile solo attraverso simulazioni numeriche, dal momento che l’analisi di stabilità
lineare non permette di identificare la soglia oltre la quale si ha la transizione poiché
tutte le traiettorie sono asintoticamente stabili in entrambi i regimi. Riportiamo di
seguito i principali risultati numerici conseguiti da Zillmer et al. [12].
Nel modello di rete LIF studiato in [12], lo stato dell’i-esimo neurone è completamente determinato dal potenziale di membrana Vi (t̃) ed obbedisce all’equazione
τm V̇i = a − Vi − τm (Vi + W )
N X
X
j=1 k
(k)
gij δ(t̃ − t̃j ) ,
(3.39)
dove N è il numero di neuroni, τm è la costante di tempo di membrana, a è la corrente
in ingresso soprasoglia (che si riferisce ad una resistenza di membrana unitaria) e W
è il potenziale di inversione. Ogniqualvolta il potenziale Vj (t̃) raggiunge il valore di
soglia Θ, viene riassegnato al valore R < Θ e viene emesso un impulso; tale impulso
è ricevuto istantaneamente da tutti i neuroni connessi a quello che ha emesso un
(k)
impulso, al tempo t̃j (k identifica l’evento di emissione del potenziale di azione del
j-esimo neurone). La ricezione dell’impulso da parte dell’i-esimo neurone provoca
un abbassamento del potenziale di membrana di tale neurone, in accordo con la
trasformazione
Vi′ + W = (Vi + W ) exp(−gij ).
(3.40)
L’ultimo ingrediente che definisce la dinamica del sistema è la matrice di connettività
gij . L’accoppiamento è riscalato con il grado di connettività del neurone che riceve
l’impulso, per cui
gij =







G/ℓi , se i e j sono connessi,
0,
(3.41)
altrimenti,
dove G è la costante di accoppiamento e li il numero di connessioni in ingresso al
neurone i. In altre parole, consideriamo il tipo più semplice di disordine, determinato dalla presenza, o dall’assenza, dei legami tra i neuroni (le autointerazioni
sono escluse). La frazione ̺m di legami mancanti è determinata fissando deterministicamente il numero totale Nm di legami recisi [Nm = ̺m N(N − 1)]; ad esempio,
scegliendo di tagliare il 5% dei legami si ha ̺m = 0.05 (caso di debole disordine).
A differenza del modello analizzato in Ref. [11], dove sono distribuite in maniera
casuale sia le costanti di accoppiamento gij , che le correnti di soglia Cij , qui l’unica sorgente di disordine è la presenza (assenza) di connessioni inibitorie. L’altra
importante differenza riguarda la costante di accoppiamento: mentre in [11] non è
ipotizzata nessuna dipendenza dalla dimensione del sistema, in questo caso è assunta
una dipendenza inversamente proporzionale dal numero di connessioni entranti.
Ci aspettiamo che il debole disordine introdotto dalla diluizione riduca l’accoppiamento efficacie tra i neuroni e faccia aumentare il valore dell’esponente di Lyapunov
massimo λ1 , rispetto al caso di neuroni completamente accoppiati. Analizzando la
figura (3.8) vediamo che l’esponente di Lyapunov massimo λ1 in effetti cresce al
crescere della frazione di legami tagliati, ma rimane negativo almeno fino a ̺m = 0.2.
Inoltre le simulazioni numeriche indicano che λ1 rimane finito nel limite termodinamico N → ∞. Dunque, prima o poi, la dinamica deve convergere verso un’orbita
periodica stabile.
In realtà le cose sono assai più complicate. In particolare, la durata media dei
transitori < ttr > necessari a raggiungere l’orbita periodica dipende dall’accoppiamento G. All’aumentare dell’accoppiamento < ttr > prima decresce e poi si
-3.8
N=100
N=200
N=300
λ1
-4
-4.2
-4.4
0
Figura 3.8.
10
0.1
0.05
ρm
Esponente di Lyapunov massimo in funzione della frazione di legami
recisi e per tre valori diversi della dimensione della rete.[12]
5
10
(a)
N=100
N=200
4
<ttr>
<ttr>
10
10
5
(b)
G=1.8
4
10
10
10
0.2
0.15
3
G=0.5
2
3
0.5
1
1.5
10
1
50
G
100
150
200
N
250
300
Figura 3.9. (a) Lunghezza media del transitorio < ttr > in funzione della costante
di accoppiamento G per due dimensioni diverse della rete. (b) Lunghezza media
del transitorio < ttr > in funzione della dimensione della rete per due valori della
costante di accoppiamento. I quadrati verdi corrispondono al valore della costante
di accoppiamento G = 0.5; i cerchi rossi a G = 1.8. In ordinata la scala usata è
logaritmica. [12]
innalza rapidamente per G ≥ 1. Inoltre all’aumentare di N il tasso di crescita è
assai maggiore, come mostrato in figura (3.9a). D’altra parte la lunghezza media
del transitorio cresce in modo diverso con N a seconda dell’accoppiamento, come
mostrato in figura (3.9b). Per G <≈ 1 < ttr > cresce linearmente con N, mentre
per G >≈ 1 esso diverge esponenzialmente.
Per G <≃ 1, l’evoluzione dinamica del sistema è simile a quella del caso completamente accoppiato. Dopo un transitorio di breve durata, il sistema converge
ad uno stato caratterizzato da una sequenza di N impulsi (emessi da tutti gli N
250
Indice di Neurone
50
Indice di Neurone
40
30
20
200
150
100
50
10
(a)
0
10250
10300
10350
10400
10450
Tempo
0
140
150
160
170
Tempo
Figura 3.10. (a) Indice del neurone che emette un impulso vs tempo per un tipico
attrattore periodico per G = 2, N = 50. (b) Indice del neurone che emette un
impulso vs tempo durante il transitorio per G = 2, N = 50. [12]
neuroni), che si ripetono periodicamente (vedi figura 3.10a). Tutti i neuroni emettono impulsi con lo stesso ritmo, ma le loro fasi sono equispaziate; in altri termini
la soluzione asintotica è uno stato asincrono. La differenza sostanziale con il caso
completamente accoppiato sta nel fatto che sequenze di impulsi differenti non sono
equivalenti l’una all’altra. Nel limite di neuroni identicamente accoppiati la dinamica è invariante sotto qualsiasi permutazione, cosa che non è più vera nel momento
in cui si introducono delle eterogeneità nella connettività della rete.
Per valori della costante di accoppiamento G ≥ 1, si manifesta un regime dinamico irregolare, dove il mutuo ordinamento cambia durante l’intero transitorio, come si
può vedere in figura (3.10b), dove compare un lento ma sistematico riaggiustamento
dell’ordine con cui i neuroni emettono impulsi successivi.
Riassumendo, la dinamica transitoria osservata per G ≈> 1: (i) è caratterizzata
da un esponente di Lyapunov negativo; (ii) è effettivamente stazionaria; (iii) ha
durate temporali esponenzialmente lunghe. Queste sono le caratteristiche distintive
del “caos stabile”, associato alla presenza di discontinuità nello spazio delle fasi [30].
Nel caso presente le discontinuità sono dovute a cambiamenti nell’ordinamento con
cui i neuroni emettono impulsi in successione, ordinamento che può cambiare a causa
della diluizione delle connessioni [32]
Capitolo 4
Dinamica di una rete neurale
eccitatoria diluita
Nei capitoli precedenti abbiamo dato un’ampia descrizione della dinamica di reti
globalmente accoppiate. La questione che ci poniamo adesso è quella di capire da
una parte, quali caratteristiche delle reti omogenee permangano con la diluizione e
dall’altra, quali differenze insorgano. Il lavoro che ci proponiamo di fare è dunque
quello di analizzare la dinamica collettiva di reti diluite con accoppiamento eccitatorio impulsivo, ove cioè l’accoppiamento fra i vari neuroni sia mediato solo dagli
impulsi. A causa della diluizione delle connessioni, effettuata in modo aleatorio,
ogni neurone riceve impulsi solo dai neuroni presinaptici a cui è connesso, quindi
la sequenza di impulsi ricevuta è diversa per ogni neurone. Nell’ambito dei modelli
matematici nel quale si collocano le reti neurali, è naturale introdurre due tipi di
diluizione e trattare parallelamente il caso di disordine quenched (temprato) e quello
di disordine annealed (ricotto)1 . Dall’analisi di reti diluite in presenza di disordine
quenched risulta che permangono alcune segnature della dinamica del sistema globalmente accoppiato ma che, nel limite termodinamico, abbiamo a che fare con un
1
Nel proseguo della tesi useremo questi anglicismi invece dei corrispondenti termini italiani
perché, ormai, sono invalsi nel linguaggio comune.
attrattore genuinamente caotico. Dall’analisi di reti con disordine annealed si ricava
invece una completa corrispondenza col sistema globalmente accoppiato nel limite
termodinamico. L’origine del caos può essere ricondotta alle minime fluttuazioni
nella periodicità dei campi autoconsistenti dei singoli neuroni, come cercheremo di
mostrare forzando un sistema di più neuroni con un campo periodico. Dunque,
anche se molte caratteristiche strutturali delle reti diluite si possono dedurre dall’analisi di campo medio effettuata in reti globalmente accoppiate, nascono anche
molte differenze già dall’introduzione di due tipi di disordine e dalla conseguente
investigazione, in parallelo, della corrispondente dinamica.
Nel primo paragrafo introdurremo il modello, oggetto della nostra analisi, che
risulta una generalizzazione di quello introdotto nel paragrafo 3.1.1, dal momento
che adesso ogni neurone è soggetto ad un campo distinto. Inoltre, analogamente a
quanto fatto in precedenza, ridurremo la dinamica della rete leaky integrate-and-fire
ad una mappa ad evento guidato. Nel secondo paragrafo ci concentreremo sull’analisi
di stabilità lineare delle soluzioni collettive che emergono in questa rete, sia nel caso
completamente accoppiato, che diluito. In particolare ci interesseremo a stati asincroni ed a regimi di sincronizzazione parziale. Nel terzo paragrafo studieremo come
l’introduzione del disordine vada a modificare lo scenario di biforcazione osservato
in reti globalmente accoppiate. Al fine di caratterizzare tale scenario di biforcazione
analizzeremo sia l’andamento dei campi che degli esponenti di Lyapunov massimi
al variare del parametro che determina l’ampiezza temporale degli impulsi. Nei
paragrafi quattro e cinque caratterizzeremo lo stato parzialmente sincronizzato dal
punto di vista dinamico, per dimensioni crescenti della rete, in presenza di disordine
quenched (paragrafo quattro) e di disordine annealed (paragrafo cinque). Vedremo
in questi paragrafi che la peculiare dinamica caotica osservata dipende dal tipo di
disordine introdotto. Nel sesto paragrafo verificheremo come si possano mettere in
corrispondenza i sistemi con disordine annealed e quelli globalmente accoppiati. In
particolare mostreremo che rescindere una precisa percentuale di legami corrisponde
a ridurre, in una rete globalmente accoppiata, la costante di accoppiamento di un
fattore pari alla percentuale di legami recisi. Infine nell’ultimo paragrafo cercheremo
di dare una spiegazione dell’origine delle dinamiche caotiche osservate. In particolare
analizzeremo la risposta del nostro sistema ad un campo periodico esterno uguale
per tutti i neuroni della rete e confronteremo quanto ottenuto con quanto trovato
nei paragrafi precedenti in presenza di un campo autoconsistente.
4.1
Modello della rete in tempo continuo
Consideriamo una rete di N neuroni LIF con accoppiamento eccitatorio mediato da
impulsi di forma Es (t) =
α2 t −αt
e
N
. La dinamica del singolo neurone è descritta da
un insieme di variabili (vi ,Ei ), dove vi descrive il potenziale di membrana del singolo
neurone, mentre Ei è il campo dovuto agli impulsi ricevuti in passato dal neurone
in oggetto. L’evoluzione dinamica del neurone i è regolata dalle seguenti equazioni
differenziali
v̇i = a − vi + gEi (t),
Ëi (t) + 2αĖi + α2 Ei (t) =
i = 1, · · · ,N
α2 X
δ(t − tn ),
N n|tn <t
(4.1)
(4.2)
dove tutte le variabili e i parametri sono espressi in unità adimensionali. Come già
sottolineato nel paragrafo (3.1.1), la condizione a > 1 corrisponde ad una corrente
soprasoglia in ingresso, mentre g rappresenta la costante di accoppiamento con il
campo autoconsistente. Nelle nostre simulazioni abbiamo fissato a = 1.3 e g = 0.4
per potersi confrontare con i risultati riportati nel lavoro seminale di van Vreeswijk
[29] sugli stati parzialmente sincronizzati in reti globalmente accoppiate. Ogni neurone dunque, in questa schematizzazione, è soggetto ad un campo forzante diverso,
generato dalla somma degli impulsi da lui ricevuti nel passato e provenienti dai
neuroni a lui connessi. Nel caso di reti globalmente accoppiate questa descrizione
è ridondante dal momento che ogni singolo neurone in esame è sottoposto agli impulsi di tutti gli altri elementi costitutivi della rete: tutti i neuroni sono identici e
rispondono agli impulsi esterni allo stesso modo, quindi i campi forzanti {Ei } sono
tutti identici. Tale descrizione diventa però fondamentale alla luce dell’introduzione
della diluizione. Nel caso di sistemi diluiti è necessario mantenere la descrizione
esplicita dei diversi campi, perché ogni neurone non risulta identico agli altri, non
avendo lo stesso grafo di connessione. Se il numero di connessioni varia da neurone
a neurone, varia anche il numero di impulsi ricevuti dai neuroni connessi in un certo
intervallo di tempo e dunque varia il campo Ei , che rappresenta la sovrapposizione
di tali impulsi.
4.1.1
Mappa ad evento guidato
Trasformiamo il sistema dinamico originale (4.1, 4.2) in una mappa tra due configurazioni successive della rete; queste corrispondono ai tempi di emissione di due
impulsi consecutivi da parte di due neuroni qualsiasi della rete. Indichiamo con tn il
tempo immediatamente successivo all’emissione dell’n-esimo impulso. Se integriamo
l’equazione (4.2) tra il tempo tn e il tempo tn+1 si ottengono le risultanti equazioni
per la mappa ad evento guidato
Ei (n + 1) = Ei (n)e−ατ (n) + Pi (n)τ (n)e−ατ (n) ,
Pi (n + 1) = Pi (n)e−ατ (n) + gk,i
α2
,
N
i = 1, · · · ,N.
(4.3)
(4.4)
dove τ (n) = tn+1 − tn è l’intervallo temporale che intercorre tra l’emissione dell’nesimo e dell’(n + 1)-esimo impulso, mentre Pi è una nuova variabile, introdotta per
semplicità e legata al campo Ei dalla relazione Pi = (αEi + Ėi ). La matrice di
connettività gij tiene conto della presenza o meno del legame tra il neurone j e
il neurone i; la connessione è unidirezionale e diretta da j a i. Nel caso in cui il
legame sussista scegliamo gij = 1, altrimenti gij = 0. Ovviamente nel caso di reti
globalmente connesse gij sarà sempre 1. Nella mappa (4.4) compare uno specifico
indice per la matrice di connessione, k; tale indice identifica il neurone più vicino a
soglia, ovvero rappresenta l’indice del neurone che sparerà al tempo tn+1 . Integrando
anche la (4.1), si ottiene la terza equazione della mappa ad evento guidato (le altre
due essendo la 4.3 e la 4.4):
vi (n + 1) = vi (n)e−τ (n) + a(1 − e−τ (n) ) + gFi (n), i = 1, · · · ,N ,
(4.5)
dove Fi è data da
e−τ (n) − e−ατ (n)
Pi (n)
τ (n)e−ατ (n)
Fi (n) =
Ei (n) +
−
Pi (n) .
α−1
α−1
(α − 1)
!
(4.6)
L’intervallo di tempo τ è calcolato a partire dall’equazione trascendente
"
vk (n) − a
τ (n) = ln
1 − gFk (n) − a
#
.
(4.7)
dove l’indice k è ancora relativo al neurone più vicino a soglia. Le equazioni (4.5,
4.6) possono essere riscritte in una forma ancora più compatta, esprimendo F (n)
come una funzione di τ (n) grazie alla (4.7), cioè:
vi (n + 1) = vi (n)e−τ (n) + 1 − vk (n)e−τ (n) ,
i = 1, · · · ,N − 1 ,
(4.8)
vk (n + 1) = 0.
Un aspetto importante delle reti globalmente connesse è il fatto che l’ordine dei
potenziali di membrana si mantiene inalterato nel tempo [11]; in altri termini qualsiasi sia l’ordine iniziale degli impulsi emessi dai neuroni questo rimane inalterato col
passare del tempo, dal momento che non può essere cambiato dalla regola dinamica.
Quindi una volta ordinati i potenziali, è sufficiente stimare, ad ogni passo, la (4.7)
per il neurone successivo a quello che ha appena emesso un impulso e ripetere l’operazione ciclicamente nel tempo. Questo non è più vero in presenza di diluizione e di
N differenti campi, poiché, in questo caso, l’ordine può cambiare nel tempo. Dato
l’ordine iniziale dei potenziali, non sarà più noto l’indice del neurone più vicino a
soglia già alla seconda iterazione della mappa, per cui, ad ogni iterazione, occorre
calcolare quale degli N − 1 neuroni che non hanno sparato, è quello più prossimo
ad emettere un impulso. Questo significa risolvere, ad ogni passo di iterazione della
mappa, N − 1 equazioni trascendenti del tipo
"
vi (n) − a
τi (n) = ln
1 − gFi(n) − a
#
.
(4.9)
e vedere quale neurone k soddisfa la relazione (k : inf i {τi (n)} = τk (n)).
4.1.2
Algoritmo numerico
A livello di simulazioni numeriche, un algoritmo siffatto comporta un ingente dispendio di tempo di calcolo, per cui abbiamo implementato un algoritmo maggiormente efficiente, capace di ridurre i tempi di simulazione di un fattore 6 − 7. Tale
schema di evoluzione della mappa consiste in quattro passi principali:
1. Presi in esame tutti i potenziali dei neuroni della rete ad un certo istante,
ne riordiniamo gli indici in modo che i valori dei corrispondenti potenziali
compaiano in ordine decrescente. In altri termini registriamo gli indici dei
neuroni in modo che l’indice del neurone più vicino a soglia sia il primo della
lista, l’indice del secondo neurone più vicino a soglia compaia al secondo posto
nella lista e cosı̀ via.
2. Calcoliamo il minimo τi (n) risolvendo l’equazione trascendente (4.9) solo per
una frazione M = N/10 di neuroni. I neuroni selezionati per effettuare tale
calcolo sono i primi M neuroni della lista precedente.
3. Facciamo evolvere la mappa per un numero di iterate minore di M, tipicamente
I = M/4. L’evoluzione della mappa interessa tutti gli N neuroni della rete,
mentre il calcolo dei tempi necessari ai neuroni per arrivare a soglia (e di
conseguenza la stima del tempo più piccolo) continua ad interessare solo gli
M neuroni selezionati al punto (2).
4. Dopo I passi di aggiornamento della mappa, si riordinano nuovamente i potenziali e si procede ripercorrendo i passi precedenti.
Prendendo in esame solo il blocco dei primi M neuroni per calcolare i tempi minimi
di raggiungimento della soglia, corriamo il rischio di trascurare eventi rilevanti e
di considerare invece eventi fittizi. Occorre dunque cautelarsi da eventuali sorpassi
effettuati dai neuroni non contenuti nel blocco degli M neuroni selezionati al passo
(2). Per fare questo abbiamo ulteriormente raffinato l’algoritmo tenendo conto del
fatto che, ogniqualvolta un neurone emette un impulso, il suo potenziale di membrana viene riazzerato. Di conseguenza dopo ogni iterata della mappa abbiamo
posto l’indice del neurone che ha appena emesso un impulso in fondo alla lista dei
potenziali ordinati, fuori dunque dal blocco dei primi M. Abbiamo cosı̀ inserito al
suo posto, nel sottoinsieme su cui calcolare i tempi minimi di raggiungimento della
soglia, il primo neurone della lista ordinata che si trova dopo gli M del gruppo selezionato. Possiamo cosı̀ lavorare sempre su un sottoinsieme di dimensione costante
M (< N), su cui calcolare, per I iterate, i tempi necessari ai neuroni per arrivare a
soglia e, contemporaneamente, essere sicuri di tenere sotto controllo sempre i neuroni
più vicini a soglia.
4.1.3
Scelta aleatoria delle connessioni
La scelta delle connessioni nel caso diluito viene fatta in modo aleatorio quindi,
dato che non tutte le connessioni sono attive, ciò introduce del disordine nel sistema. Questo disordine può essere inserito nella matrice di accoppiamento gij in
due diversi modi: disordine quenched (temprato) o annealed (ricotto) [1]. Queste
definizioni rimandano alla tecnica della tempra (quench) in cui un metallo viene
raffreddato rapidamente per aumentarne la durezza. Il procedimento con cui un
metallo temprato viene riportato ad alta temperatura e poi raffreddato lentamente
per renderlo più malleabile è invece detto ricottura (annealing). Nel nostro caso
il disordine quenched corrisponde ad un grafo di connessione aleatorio definito una
volta per tutte prima di far evolvere la mappa, mentre con disordine annealed indichiamo la riassegnazione aleatoria delle connessioni tra i neuroni (e le eventuali
disconnessioni) ad ogni passo di iterazione della mappa. Per quanto riguarda l’implementazione numerica del disordine quenched agli elementi della matrice gij , si
assegna il valore 0, 1 con una certa probabilità ν, che dipende dalla percentuale di
legami che vogliamo recidere; tale assegnazione viene effettuata all’inizio del programma, prima di far evolvere la mappa. Per quanto riguarda invece il disordine
annealed, l’assegnazione dei valori 0, 1 agli elementi di matrice avviene all’interno
dell’algoritmo di evoluzione della mappa, sempre con una certa probabilità ν fissata,
prima di ogni passo di evoluzione. Ad ogni passo di aggiornamento della mappa i
neuroni possono dunque essere connessi in modo diverso con gli altri neuroni della
rete, ma la percentuale di neuroni presinaptici in media è ν. In presenza di disordine quenched occorre comunque definire una matrice di connessione di dimensione
N × N. In questo caso dobbiamo dunque confrontarci con i limiti di memoria dei
calcolatori che non ci permettono di estendere le simulazioni a reti arbitrariamente
grandi. In presenza di disordine annealed possiamo ovviare a questo problema dal
momento che nelle equazioni della mappa ad evento guidato (4.3, 4.4, 4.8) compare
solo la riga gk,i della matrice di connessione. Questo ci permette di introdurre un
vettore di dimensione N che identifica ad ogni iterata le connessioni tra il neurone k
più vicino a soglia e gli altri N − 1 neuroni della rete. Lavorando con un vettore di
dimensione N che viene ridefinito ad ogni passo di evoluzione della mappa, piuttosto
che con una matrice N × N abbiamo un notevole risparmio di memoria. Nel caso
di disordine annealed questo ci consente dunque di implementare reti di dimensioni
maggiori rispetto al caso quenched.
4.2
Analisi di stabilità lineare
Per l’analisi di stabilità lineare si deve considerare l’evoluzione dinamica delle perturbazioni; ciò si ottiene linearizzando le equazioni della mappa (4.3, 4.4, 4.8), in
modo da ottenere l’evoluzione di tali perturbazioni nello spazio tangente:
δEi (n + 1) = e−ατ (n) δEi (n) + τ (n)e−ατ (n) δPi (n)
(4.10)
− [αEi (n) − Pi (n) + ατ (n)Pi (n)]e−ατ (n) δτ (n),
δPi (n + 1) = e−ατ (n) δPi (n) − αPi (n)e−ατ (n) δτ (n),
(4.11)
δvi (n + 1) = e−τ (n) (δvi (n) − δvk (n)) − (vi (n) − vk (n))e−τ (n) δτ (n),
(4.12)
i = 1, · · · ,N − 1,
δvk (n + 1) ≡ 0,
(4.13)
con
δτ (n) =
(
δPk (n)
e−τ (n) − e−ατ (n)
e−τ (n) − e−ατ (n)
δEk (n) +
− τ (n)e−ατ (n)
·
α−1
α−1
α−1
1
"
(
·
δvk (n)
g
+
·
vk (n) − a 1 − gFk (n) − a
1−
g
1−gFk (n)−a
n
αe−ατ (n) −e−τ (n)
α−1
h
Ek (n) +
Pk (n)
α−1
i
−
e−ατ (n) Pk (n)
α−1
+
#
))
ατ (n)e−ατ (n)
Pk (n)
α−1
(4.14)
o.
Indicando con δu = (δE1 , · · · ,δEN ,δP1 , · · · ,δPN ,δv1 , · · · ,δvN ) il vettore dello spazio
tangente, è possibile definire la matrice di evoluzione Φ a partire dalle equazioni
(4.10,4.11,4.12) come δu(n + 1) = Φδu(n) 2 . Possiamo effettuare a questo punto
una stima dell’esponente massimo e dello spettro di Lyapunov della rete, che costituiscono gli indicatori di caos maggiormente efficaci per descrivere sistemi con molti
gradi di libertà. Si ricorda che un sistema si dice caotico se il massimo esponente
di Lyapunov risulta positivo [33]. Lo spettro di Lyapunov {λj }, j = 1, · · · ,3N − 1
2
Si noti che Φ viene calcolata sulla traiettoria del sistema di equazioni (4.3, 4.4, 4.5).
0
λ0j
-0.002
−1
-0.004
λj
−2
-0.006
0
10
20
30
40
j
−3
−4
(a)
0
100
50
150
j
0
λj
0
-2
-0.001
-4
λj
-0.002
-6
0
5
10
-8
j
15
-10
-12
(b)
0
100
50
150
j
Figura 4.1. Spettro di Lyapunov per una rete globalmente connessa di N = 50
neuroni. Gli spettri presentati sono ordinati in modo decrescente, dunque gli esponenti vanno dal più grande (in alto a sinistra), al più piccolo (in basso a destra).
(a) Le simulazioni sono state effettuate prendendo come valori dei parametri α = 3,
g = 0.4, a = 1.3. L’inserto mostra come gli esponenti di Lyapunov della prima
banda siano tutti negativi e si presentino a coppie. (b) I valori dei parametri sono
gli stessi di quelli utilizzati per la simulazione in (a), a parte α che, in questo caso,
vale 9. L’inserto mostra come l’esponente di Lyapunov massimo sia nullo.
è stimato numericamente dal tasso di crescita esponenziale del modulo degli autovalori della matrice di evoluzione nello spazio tangente, ove, per aumentare la precisione numerica, gli autovettori vengono periodicamente ortonormalizzati secondo lo
schema di Gram-Schmidt [34, 35] (si veda l’appendice C.2 per una descrizione più
dettagliata di questi indicatori e della loro stima numerica).
4.2.1
Reti globalmente accoppiate
Per prima cosa stimiamo gli spettri di Lyapunov per reti globalmente accoppiate; in
particolare analizziamo la figura (4.1) in cui sono riportati gli spettri completi di reti
neurali composte da N = 50 neuroni globalmente accoppiati. In figura (4.1a) è riportato lo spettro relativo al regime di stato asincrono (α = 3), mentre in figura (4.1b)
sono presentati i risultati delle simulazioni numeriche in regime di sincronizzazione
parziale (α = 9) (vedi paragrafo 3.2.4). In entrambi i casi lo spettro è composto da
due bande più due autovalori isolati: la banda superiore corrisponde alla dinamica dei vi , i = 1, · · · ,N − 1, mentre i due autovalori isolati sono associati ai campi
(E, P ) non ridondanti e corrispondenti ai due autovalori isolati di Floquet presenti
in figura (3.2); infine la seconda banda corrisponde all’evoluzione dei campi {Ei , Pi }
ridondanti e tutti identici tra loro. Nel caso di una rete globalmente connessa di
dimensione N, le variabili indipendenti sono N + 1; tali variabili indipendenti sono
i potenziali di membrana v1 , · · · ,vN −1 ed i campi E1 , P1 3 . Nel caso della mappa
ad evento guidato da noi considerata, (equazioni 4.3, 4.4, 4.8), le variabili in gioco
sono 3N − 1. In questo caso infatti abbiamo a che fare con i potenziali di membrana v1 , · · · ,vN −1 e con i campi E1 , · · · ,EN ,P1 , · · · ,PN , dal momento che un grado
di libertà viene rimosso grazie alla sezione di Poincaré anche nel caso globalmente
accoppiato. Questo significa che 2(N − 1) variabili sono ridondanti e che queste
sono E2 , · · · ,EN , P2 , · · · ,PN . Si può dimostrare che il valore dei 2(N − 1) esponenti
di Lyapunov associati alle variabili ridondanti è λl = −α, per l = 1, · · · ,2(N − 1).
Per dimostrarlo e per calcolare il valore degli esponenti di Lyapunov della seconda
banda procediamo nel seguente modo. Supponiamo che (E1 , P1 ) sia la coppia di
variabili non ridondanti e studiamo la dinamica degli altri campi rispetto a questa
3
Possiamo scegliere come indice dei campi non ridondanti 1 senza perdita di generalità.
coppia introducendo le variabili differenza
wi = Ei − E1
zi = Pi − P1
i = 2, · · · ,N
(4.15)
Le equazioni di evoluzione per le variabili differenza sono
wi (n + 1) = wi (n)e−ατ (n) + zi (n)τ (n)e−ατ (n)
zi (n + 1) = zi (n)e−ατ (n) + gk,i
α2
N
(4.16)
i = 2, · · · ,N.
(4.17)
Per effettuare l’analisi di stabilità lineare consideriamo, come di consueto, l’evoluzione
dinamica delle perturbazioni e differenziamo le equazioni precedenti. Si ottiene
δwi (n + 1) = δwi (n)e−ατ (n) + δzi (n)τ (n)e−ατ (n)
(4.18)
δzi (n + 1) = δzi (n)e−ατ (n)
(4.19)
i = 2, · · · ,N,
o, in forma matriciale





δwi 
δzi



n+1

=

−ατ
−ατ
e
τe
−ατ
0
e





δwi 
δzi



n

=Ψ


δwi 
δzi


(4.20)
n
Risolvendo l’equazione agli autovalori per la matrice d’evoluzione Ψ , con unità di
tempo τ

det[Ψ − e−λτ I] = det 


−ατ
e
−λτ
−e
0
−ατ
τe
e−ατ − e−λτ




=0
(4.21)
si ottiene (λ + α)2 = 0, quindi λ = −α con degenerazione 2. Inoltre, dato che abbiamo svolto la dimostrazione con un indice i generico, si ottiene che gli esponenti
valgono tutti λl = −α per l = 1, · · · ,2(N − 1). Questi esponenti corrispondono agli
esponenti di Lyapunov trasversi nello studio della sincronizzazione dei sistemi dinamici [36, 37] in quanto misurano il tasso di convergenza esponenziale verso lo stato
sincronizzato in cui tutti i campi sono uguali a causa dell’accoppiamento globale.
Dunque tutte le variabili si sincronizzano tra loro e, dal momento che l’autovalore
è negativo, si sincronizzano con la dinamica della coppia (E1 , P1 ). Questo spiega
perché otteniamo in figura (4.1) una banda pari a −α sia nello stato asincrono che
nello stato parzialmente sincronizzato.
Focalizziamo adesso la nostra attenzione sull’inserto della figura (4.1b), dove
abbiamo evidenziato l’andamento degli esponenti di Lyapunov in prossimità dello
zero. L’esponente di Lyapunov massimo λ1 è zero, mentre gli altri sono tutti negativi; questo significa che abbiamo a che fare con una dinamica quasiperiodica. Gli
esponenti di Lyapunov nulli del sistema a tempo continuo sono in realtà due, ma uno
di essi viene eliminato passando al tempo discreto a causa della sezione di Poincaré
effettuata. In figura (4.1a) invece gli esponenti sono tutti negativi, come si vede
chiaramente nell’inserto, e l’unico esponente nullo, tipico di uno stato periodico, è
stato rimosso in virtù del passaggio al tempo discreto.
Indaghiamo adesso l’esistenza di eventuali leggi di scala che caratterizzino gli
spettri di Lyapunov per reti globalmente accoppiate al variare del numero di neuroni
N della rete. Limitiamo la nostra analisi a due casi specifici: reti neurali con a = 1.3,
g = 0.4 e α = 3 che si trovano nello stato asincrono e reti con a = 1.3, g = 0.4
e α = 9 che sono caratterizzate da un regime di sincronizzazione parziale (vedi
paragrafo 3.2.4). Nel caso α = 3 ci aspettiamo che gli spettri di Lyapunov scalino
come 1/N 2 dal momento che già gli esponenti di Floquet associati alle componenti
di lunghezza d’onda breve mostrano tale dipendenza da N (vedi paragrafo 3.2.2). I
risultati di simulazioni numeriche (vedi figura 4.2a) ci confermano la validità di tale
legge di scala al variare di N per reti neurali che si trovino nello stato asincrono. In
particolare, tali risultati ci dicono che gli spettri degli esponenti di Lyapunov, per
α = 3, una volta moltiplicati per N 2 , collassano su una curva universale quando siano
riportati in funzione di una variabile riscalata j/N, dove j è l’indice dell’esponente
di Lyapunov, una volta che lo spettro sia stato ordinato in maniera decrescente. Nel
caso di reti in regime di sincronizzazione parziale (α = 9) tale legge di scala sembra
-0.4
(b)
(a)
-5
-0.5
-0.6
2
λj N
λj N
2
-6
-0.7
-7
-0.8
N=50
N=100
N=200
-0.9
N=50
N=100
N=200
-8
-1
0
0.1
0.2
0.3
0.4
-9
0.5
0
0.1
0.2
j/N
0.3
0.4
0.5
j/N
Figura 4.2. Analisi del riscalamento degli spettri di Lyapunov per sistemi di dimensione diversa (N = 50,100,200). Gli spettri originali, ordinati in maniera decrescente, sono riportati in funzione della variabile riscalata j/N , dove j è l’indice
dell’esponente di Lyapunov. In ordinata gli esponenti sono moltiplicati per N 2 .
Per maggiore chiarezza è riportata solo la prima banda dello spettro. (a) Le reti
indagate sono globalmente connesse e in regime di stato asincrono (α = 3). (b)
Le simulazioni interessano reti globalmente connesse in regime di sincronizzazione
parziale (α = 9). L’autovalore massimo, che vale per tutte e tre le realizzazioni
di reti 0, è stato omesso dalla figura, in modo da visualizzare meglio l’andamento
della parte restante dello spettro riportata.
0.06
0.012
λ1
λ1
0.05
0.01
0.008
0.04
0.006
0.03
0.004
0.02
0.002
0
0.01
(a)
0
0.1
0.2
Percentuale di legami recisi
(b)
0.3
0
0
0.1
0.2
0.3
Percentuale di legami recisi
Figura 4.3. Andamento dell’esponente di Lyapunov massimo in funzione della
percentuale di legami recisi. Le simulazioni sono state fatte utilizzando una rete
di N = 200 neuroni in presenza di disordine quenched. I risultati presentati interessano due diversi valori del parametro α: in figura (a) è stato utilizzato α = 3; in
figura (b) invece α = 9. In entrambi i casi a = 1.3 e g = 0.4.
essere verificata solo per grandi dimensioni della rete; i risultati numerici sembrano
indicare infatti che gli spettri collassino anche in questo caso su una curva universale
solo per N sufficientemente grandi (vedi figura 4.2b)
4.2.2
Reti diluite
Passiamo ora a reti diluite e vediamo come varia l’esponente di Lyapunov massimo
λ1 in funzione della percentuale di legami recisi. Non appena i neuroni non sono
40
0%
1%
5%
10%
20%
25%
30
P
20
10
0
0
1
0.5
2
1.5
2.5
E
Figura 4.4. Andamento della variabile P̄ in funzione del campo Ē al variare della
percentuale di legami recisi. Le simulazioni interessano una rete di N = 1600
neuroni, in presenza di disordine annealed. I parametri usati sono α = 9, a = 1.3
e g = 0.4.
0.02
(a)
(b)
0
0
0
0
λj
-0.02
λj
-1
-2
λj
-0.04
-0.05
-5
λj
-0.1
-3
-10
-4
-0.06
-0.15
50
0
10
j
100
0
150
20
30
j
40
50
0
50
10
j
100
150
20
30
40
50
j
Figura 4.5. Spettro di Lyapunov per una rete diluita composta da N = 50 neuroni. Gli esponenti di Lyapunov λj sono ordinati in maniera decrescente. (a) I
risultati si riferiscono ad α = 3. (b) I risultati di simulazioni numeriche interessano
reti caratterizzate da α = 9. In entrambi i casi si ha una diluizione del 20%, la
presenza di disordine quenched ed inoltre g = 0.4 e a = 1.3.
più equivalenti tra loro, ovvero non appena alcune connessioni vengono meno, il
sistema diventa caotico e l’esponente massimo diventa positivo, come si può vedere
in figura (4.3). Fissata la dimensione della rete, si osserva che il valore dell’esponente
di Lyapunov massimo aumenta all’aumentare della diluizione, sia nel caso α = 3
(figura 4.3a), che nel caso α = 9 (figura 4.3b) 4 . All’aumentare della percentuale di
legami recisi varia anche la forma dell’attrattore, come si può vedere in figura (4.4).
4
Per calcolare le barre di errore abbiamo stimato l’esponente di Lyapunov massimo, a parità
del valore dei parametri e della percentuale di diluizione, a partire da dieci configurazioni iniziali
diverse della rete e dunque a partire da dieci realizzazioni del disordine diverse. Le barre di errore
rappresentano la deviazione standard su questi dieci valori ottenuti per l’esponente massimo.
In questa figura riportiamo l’andamento della variabile P̄ in funzione del campo Ē
per molti tempi successivi; tali variabili sono ottenute mediando, ad ogni passo di
integrazione della mappa, {Ei , Pi } fra tutti i neuroni, cioè
Ē(n) =
PN
Ei (n)
,
N
i=1
P̄ (n) =
PN
Pi (n)
.
N
i=1
(4.22)
Solo nel caso di una diluizione minima, pari all’1% dei legami totali, la forma dell’attrattore è simile a quella del sistem globalmente accoppiato, anche se aumentano sia l’ampiezza del campo Ē, che quella della variabile P̄ ; per diluizioni superiori l’ampiezza del campo Ē diminuisce, mentre aumenta quella della variabile
P̄ . Le curve si deformano, si allargano e tendono ad esplorare, all’aumentare della diluizione, la parte del piano caratterizzata da piccoli valori di Ē. Si ricorda
che grandi valori del campo corrispondono a neuroni che emettono impulsi a tempi
ravvicinati, mentre piccoli valori sono associati ad emissioni decorrelate.
Analizziamo adesso gli spettri di Lyapunov per una rete diluita di N = 50
neuroni (vedi figura 4.5). Come nel caso globalmente accoppiato, anche in questo
caso sono presenti due bande distinte e due autovalori isolati; la banda superiore è
quella relativa alla dinamica dei vi , mentre quella inferiore deriva dalla dinamica dei
campi Ei , Pi . L’introduzione del disordine nella rete, dovuto alla diluizione, fa sı̀ che
la seconda banda non sia più una retta orizzontale di valore esattamente pari a −α,
come era in figura (4.1). In questo caso gli autovalori della banda assumono valori
prossimi a −α, dato che, a causa dell’introduzione della diluizione, non ci sono più
variabili ridondanti ed i campi {Ei , Pi }, per i = 1, · · · ,N, sono tutti indipendenti
e diversi tra loro. Sia in figura (4.5a) che in (4.5b) è evidenziata la struttura della
banda superiore, mentre, in piccolo, è riportato l’intero spettro. Si nota che un
numero finito di esponenti di Lyapunov è positivo; questo significa che il caos è
alto-dimensionale, dal momento che il numero di esponenti positivi corrisponde al
numero di gradi di libertà attivi del sistema [33]. In particolare la dimensione di
Kaplan-Yorke del sistema Dky (che fornisce una stima delle dimensioni dell’attrattore
caotico, vedi appendice C.2.2 per maggiori dettagli) è pari a Dky = 45.3 nel caso
α = 3 ed a Dky = 37.0 nel caso α = 9.
4.3
Diagramma di biforcazione
In questo paragrafo studieremo come l’introduzione del disordine vada a modificare lo scenario di biforcazione osservato in reti omogenee globalmente accoppiate
(vedi paragrafo 3.2.3). Vogliamo indagare inoltre quanto sia robusto rispetto alla
diluizione lo stato parzialmente sincronizzato del sistema globalmente accoppiato.
Ci limiteremo a considerare come valori dei parametri g = 0.4 ed a = 1.3, che corrispondono a quelli utilizzati da van Vreeswijk nel suo articolo del 1996 [29]; con tali
parametri van Vreeswijk verificò, per reti globalmente accoppiate, la presenza di una
transizione dallo stato asincrono allo stato parzialmente sincronizzato in corrispondenza di un valore di α pari ad αc = 8.34 ± 0.01. Questa analisi è stata estesa da
Zillmer et al. [10] a tutto l’intervallo dei valori di g. Questo ci consente dunque di
dare una stima della variazione del valore di αc dovuta alla presenza della diluizione
nella rete. Se supponiamo che alla diluizione possa corrispondere, in una rete omogenea, una diminuizione del parametro di accoppiamento g di una percentuale pari
a quella dei legami recisi, possiamo stimare, a priori, il valore di αc per reti diluite,
utilizzando i risultati numerici ottenuti per reti globalmente connesse [10]. Consideriamo dunque una rete con il 20% di legami recisi. Essa corrisponderebbe ad una
rete omogenea con un accoppiamento riscalato pari a gr = 0.32 invece di 0.4. Quindi, a partire dal diagramma di fase (3.3) si ottiene che il valore di ᾱc corrispondente
a tale gr è ᾱc = 6.8 ± 0.4.
Proseguiamo la nostra analisi confrontando alcuni risultati ottenuti per reti
diluite e per reti omogenee. Abbiamo già ampiamente discusso del caso di reti
40
3
5
6
6.7
7
9
11
30
P(v)
(a)
20
10
0
0
0.2
0.4
v
0.6
0.8
1
Figura 4.6. (a) Andamento della densità di probabilità P (v) in funzione del potenziale di membrana v. Facendo riferimento al diagramma di fase (3.3) descritto nel
paragrafo (3.2.3), sappiamo che si ha una transizione per ᾱc = 6.8 ± 0.4, in corrispondenza di gr = 0.32. (b) Andamento del campo P̄ in funzione del campo Ē
al variare della costante α. I dati riportati si riferiscono ad una rete globalmente
connessa con N = 1600 neuroni, gr = 0.32 e a = 1.3.
globalmente accoppiate, ma vogliamo presentare in questo paragrafo una diversa descrizione dell’attrattore e l’andamento della densità di probabilità P (v) del
potenziale di membrana v. Il calcolo della densità di probabilità P (v) ci permette
di analizzare la sincronizzazione dei neuroni e la formazione di raggruppamenti. Per
studiare la situazione di massima sincronizzazione, la densità di probabilità P (v) è
calcolata, qui come nel resto della tesi, a tempi successivi corrispondenti ai massimi
del campo Ē. Questo equivale ad effettuare campionamenti successivi in situazioni
analoghe della rete; in altre parole la condizione di massimo ci consente di effettuare una sezione di Poincaré dell’evoluzione dinamica dei potenziali di membrana.
La scelta dei punti di massimo del campo Ē non è casuale se vogliamo studiare
la situazione di massima sincronizzazione, infatti il singolo campo Ei costituisce la
sovrapposizione lineare degli impulsi ricevuti dall’i-esimo neurone, quindi tanto più
Ē è elevato, tanti più neuroni emettono impulsi in sincronia.
Nel caso di rete globalmente connessa (vedi figura 4.6a) passiamo da una densità
di probabilità pressoché omogenea per α < ᾱc , tipica dello stato asincrono, a curve
estremamente localizzate per α ≥ 9; questo significa che al crescere di α si ha una
tendenza ad aumentare la sincronia e già per α = 9, si realizza uno stato quasi
3
5
6
6.7
7
9
11
12
10
8
P(v)
(a)
6
4
2
0
0.2
0.4
v
0.6
0.8
1
Figura 4.7. (a) Andamento della densità di probabilità P (v) in funzione del potenziale di membrana v, al variare della costante α. (b) Andamento del campo P̄ in
funzione del campo Ē al variare della costante α. I dati riportati si riferiscono
ad una rete con N = 1600 neuroni, con il 20% di legami rotti e in presenza di
disordine quenched; inoltre g = 0.4 e a = 1.3.
sincronizzato. Le curve estremamente localizzate ottenute per α > 9 indicano anche
la presenza di un chiaro raggruppamento di neuroni (vedi figura 4.6a per α = 11).
Nel caso di rete diluita con disordine quenched (vedi figura 4.7) lo scenario è simile
e anche in questo caso si può notare la transizione da uno stato che ricorda lo stato
asincrono ad uno stato assimilabile a quello parzialmente sincronizzato. Non possiamo parlare propriamente di stato asincrono o di stato parzialmente sincronizzato
in presenza di diluizione, dal momento che gli stati, in questo nuovo scenario, sono
caotici. Abbiamo dunque a che fare con stati diversi da quelli che caratterizzano la
dinamica di reti globalmente accoppiate; nonostante ciò alcune caratteristiche della
dinamica microscopica associata all’evoluzione dei vi e delle variabili Ei , Pi , si mantengono anche in presenza di diluizione. L’introduzione del disordine fa sı̀ che la
curva P (v) sia molto meno localizzata e liscia ad α = 9 rispetto al caso precedente,
ma rimane una chiara indicazione dell’aumento del grado di sincronizzazione.
Per caratterizzare la forma dell’attrattore che descrive la dinamica collettiva della rete riportiamo ora i valori delle variabili Ē, P̄ , a vari istanti di tempo, nel piano
(Ē,P̄ ). Nel caso di rete globalmente accoppiata (vedi figura 4.6b) la forma dell’attrattore varia al crescere di α; per α < ᾱc gli attrattori sono punti fissi stabili,
mentre per α > ᾱc divengono orbite periodiche stabili la cui forma varia con α. Nel
caso di una rete diluita quenched (vedi figura 4.7) si osserva uno scenario analogo:
per α < ᾱc al punto fisso si sostituisce un attrattore caotico che forma una nube di
punti, mentre per α > ᾱc l’attrattore si sviluppa intorno ad una curva chiusa, che
cambia al variare di α. A parità di dimensioni della rete e del valore parametro a
ed utilizzando una costante di accoppiamento opportunamente riscalata, osserviamo
che queste curve chiuse non coincidono con le orbite della rete globalmente connessa.
Ad ogni modo l’immagine della dinamica della rete globalmente accoppiata rimane
min E, max E
4
Fase I
3
Fase II
2
1
0
0
5
αc
10
15
α
20
Figura 4.8. Diagramma di biforcazione per il passaggio da un apparente punto
fisso stabile ad un’orbita simil-periodica stabile in corrispondenza di un valore ᾱc .
I punti rossi rappresentano i valori di massimo del campo Ē, mentre i punti neri
corrispondono ai valori di minimo assunti dal campo Ē. Ogni coppia di valori si
riferisce ai risultati delle simulazioni per un singolo valore di α. Le barre di errore
non sono state riportate in quanto minori delle dimensioni dei simboli usati. Le
simulazioni effettuate si riferiscono ad una rete con N = 1600 neuroni in presenza
di disordine quenched e con il 20% di legami recisi; inoltre g = 0.4 e a = 1.3. La
linea tratteggiata si riferisce al valore di α¯c (vedi testo per maggiori dettagli).
analoga a quella della rete diluita. Questo è dovuto al fatto che gli attrattori caotici
rimangono localizzati in prossimità degli attrattori del sistema non disordinato. La
diluizione produce quindi caos su scale relativamente piccole vista la localizzazione
dell’attrattore caotico. Ha senso dunque estendere il diagramma di biforcazione al
caso di rete diluita. Tale diagramma è mostrato in figura (4.8) assieme al valore ᾱc
di cui abbiamo discusso in precedenza. Per costruire tale diagramma di biforcazione
abbiamo riportato i valori massimi e minimi ottenuti, per ogni valore di α, per il
campo Ē 5 . In questo modo possiamo dedurre quali sono le soluzioni della dinamica
del sistema. Per α < ᾱc i valori massimi e minimi di Ē assumono valori molto prossimi tra loro mentre per α ≥ ᾱc i due valori sono assolutamente non coincidenti. Il
diagramma di biforcazione cosı̀ ottenuto risulta simile a quello riportato nella figura
(3.3). Più precisamente si osserva una transizione da un “quasi punto fisso” (cioè
l’attrattore dato dalla nube di punti per α < ᾱc ) ad una “quasi orbita periodica”
(rappresentata dalla nube di punti attorno all’orbita periodica per α > ᾱc ). In realtà questo abuso di linguaggio risulta naturale nella descrizione dell’analogia tra il
caso globalmente accoppiato e quello diluito: in quest’ultima situazione si ottengono
attrattori che, seppur caotici, rimangono prossimi a quelli del caso marginalmente
stabile e stabile.
In seguito ci riferiremo, unicamente per semplificare la notazione, agli stati ottenuti per α < ᾱc e corrispondenti al “quasi punto fisso” come a “stati della fase
I”, mentre ci riferiremo agli stati ottenuti per α > ᾱc come a “stati della fase II”.
Entriamo ora in dettaglio considerando un solo stato nella fase I corrispondente ad
α = 3 ed uno solo nella fase II corrispondente ad α = 9.
In una rete omogenea in regime di stato asincrono i campi associati ai singoli neuroni sono costanti nel tempo ed identici fra di loro. Nel caso diluito per α = 3, come
mostrato in figura (4.9a), i singoli campi mostrano piccole oscillazioni nel tempo e
sono distinti. Il disordine ha quindi un effetto chiaramente visibile nella dinamica di
questo stato. In uno stato asincrono esatto i neuroni emettono potenziali di azione
in modo temporalmente equispaziato; la presenza di disordine quenched (vedi figura
4.10a) fa sı̀ che i potenziali di membrana non siano più equispaziati ed alcuni neuroni
tendano a raggrupparsi. Queste sono le caratteristiche del comportamento caotico
del modello diluito che comunque lo mantengono prossimo al comportamento di
5
I minimi ed i massimi di Ē riportati in figura (4.8) sono stati stimati identificando i punti
estremali di Ē nel tempo e calcolandone le relative medie e deviazioni standard. In particolare
abbiamo considerato una sequenza temporale di Ē contenente 3100 minimi e massimi.
2
(a)
0.88
(b)
1.5
0.86
E
E
1
0.84
0.82
0.5
0.8
272
274
276
278
261
261.5
262
Tempo
262.5
263
Tempo
Figura 4.9. Andamento del campo esterno in funzione del tempo. (a) I risultati
si riferiscono ad α = 3. Mentre le linee continue nera, verde ed arancione si
riferiscono a campi di singolo neurone, la linea tratteggiata magenta si riferisce al
campo medio Ē. (b) I risultati si riferiscono ad α = 9. Le linee continue viola,
azzurro e magenta si riferiscono a campi di singolo neurone, mentre la linea nera,
tratteggiata, si riferisce al campo medio Ē. In entrambi i casi si ha una a che fare
con una rete con N = 400 neuroni, con disordine quenched e diluizione del 20%;
inoltre g = 0.4 e a = 1.3.
1
1
0.8
0.8
0.6
0.6
V
V
0.4
0.4
0.2
0.2
(a)
0
140
140.5
141
141.5
Tempo
142
(b)
0
271.5
272
273
272.5
273.5
274
Tempo
Figura 4.10. Andamento di alcuni potenziali di membrana di singolo neurone
in funzione del tempo. (a) I risultati di simulazioni numeriche interessano reti
caratterizzate da α = 3. (b) I risultati interessano reti caratterizzate da α = 9. In
entrambi i casi la rete analizzata è composta da N = 400 neuroni, in presenza di
disordine quenched, con una diluizione del 20% ed inoltre con g = 0.4 e a = 1.3.
quello globalmente accoppiato.
In corrispondenza di un regime di sincronizzazione parziale proprio della rete
accoppiata otteniamo un andamento periodico per i campi Ei di singolo neurone.
In una rete diluita si osserva una dinamica caotica corrispondente ad un attrattore
localizzato nell’intorno di quello della rete globalmente accoppiata. Come mostrato
in figura (4.9b) per α = 9, anche in questo caso sono presenti scarti e fluttuazioni
tra i singoli campi e il campo medio, analoghe a quelle trovate per α = 3, ma non
sono visibili su questa scala data l’ampiezza delle oscillazioni dei campi. Per α = 9
0.06
λ1
0.05
0.04
Fase I
0.03
Fase II
0.02
0.01
0
0
5
αc
10
α
15
Figura 4.11. Andamento dell’esponente di Lyapunov massimo in funzione di α.
Le simulazioni effettuate si riferiscono ad una rete con N = 200 neuroni, in presenza
di disordine quenched e con il 20% di legami recisi; inoltre g = 0.4 e a = 1.3. La
linea tratteggiata si riferisce al valore stimato di ᾱc .
inoltre i potenziali di membrana risultano più in fase rispetto al caso α = 3, ma sono
comunque diversi da neurone a neurone (vedi figura 4.10b). Ciò è dovuto al fatto che,
nello stato parzialmente sincronizzato, i potenziali di membrana emettono i rispettivi
potenziali di azione quasi contemporaneamente (questo spiega anche perché i campi
Ei siano cosı̀ grandi rispetto al caso di stato asincrono). Qualcosa di analogo, a
causa della caoticità della dinamica, avviene anche nel caso diluito.
Più in generale possiamo chiederci se lo scenario del diagramma di biforcazione
si rifletta nell’andamento degli esponenti di Lyapunov massimi che misurano con
precisione l’insorgenza del caos (vedi appendice C.2). Il diagramma di biforcazione
infatti avrebbe un significato di per sè discutibile se non fosse che gli attrattori dei
sistemi diluiti sono localizzati vicino a quelli dei sistemi non diluiti, dal momento
che, in presenza di disordine, non possiamo parlare nè di stati stabili nè di vere e
proprie fasi termodinamiche. Per avvalorare quanto ottenuto con il diagramma di
biforcazione stimiamo numericamente l’andamento dell’esponente di Lyapunov massimo, al variare di α, per reti con disordine quenched ed a partire dalla mappa ad
evento guidato introdotta nel paragrafo (4.1.1). Analizzando l’andamento dell’esponente di Lyapunov massimo λ1 in funzione di α, riportato in figura (4.11), possiamo
notare che lo stato della fase I appare debolmente caotico (λ1 ∼ 10−2 ), mentre lo
stato della fase II appare più caotico (λ1 ∼ 5 10−2 ). Se facciamo un parallelo con
quanto trovato per le reti globalmente accoppiate (paragrafo 3.2.3), vediamo che,
anche in quel caso, il passaggio dallo stato asincrono allo stato parzialmente sincronizzato comportava un aumento dell’instabilità, poiché l’esponente di Lyapunov
massimo passava da negativo (stato stabile) a nullo (stato marginalmente stabile).
Ad ogni modo troviamo, anche nel presente caso, una chiara indicazione della transizione. Il fatto che la transizione sembri avvenire in corrispondenza di un valore di
α minore di ᾱc è dovuto ad effetti di taglia finita. I risultati delle simulazioni numeriche si riferiscono infatti a sistemi con N = 200 neuroni. Effettuare simulazioni
a taglie più elevate sarebbe stato troppo dispendioso, comunque ci aspettiamo che
nel limite N → ∞ il punto di transizione coincida con ᾱc 6 .
In quanto segue ci limiteremo ad analizzare il caso α = 9, che presenta caoticità maggiore, al fine di studiare in maggior dettaglio gli effetti di differenti tipi di
disordine su uno stato dinamico collettivo della rete.
4.4
Disordine quenched
Caratterizziamo adesso uno stato della fase II dal punto di vista dinamico, in presenza di disordine quenched, per dimensioni crescenti della rete. L’ampiezza dei campi
osservata nel regime corrispondente alla fase II (vedi figura 4.9b), ci fa supporre di
aver a che fare con un raggruppamento di neuroni che viaggiano assieme. Analizzando l’andamento della densità di probabilità P (v) ci aspettiamo cosı̀ di trovare
curve sempre più localizzate all’aumentare delle dimensioni del sistema e di avere
una sincronizzazione completa nel limite termodinamico. Facendo riferimento al6
Le barre di errore riportate in figura sono calcolate utilizzando i risultati ottenuti a partire da
dieci configurazioni iniziali diverse della rete. Per ogni valore della costante α abbiamo calcolato
l’esponente di Lyapunov massimo per dieci realizzazioni diverse della rete ed abbiamo preso come
barra di errore la deviazione standard calcolata sui valori trovati per gli esponenti.
800
1600
3200
6400
12800
46000
15
Pmax
15
10
10
P(v)
0
10000
20000
30000
40000 N
5
5
(a)
0
0
0.2
0.4
v
0.6
0.8
1
Figura 4.12. (a) Andamento della densità di probabilità P (v) in funzione del
potenziale di membrana v, al variare delle dimensioni della rete. La curva tratteggiata di colore verde si riferisce all’andamento della densità di probabilità ottenuto per una rete di N = 100,000 neuroni in presenza di disordine annealed.
Nell’inserto mostriamo l’andamento dei valori assunti dalla densità di probabilità
in corrispondenza dei massimi, Pmax , in funzione di N . Le barre di errore non sono
riportate nell’inserto perché risultano minori dei simboli impiegati. La linea verde
tratteggiata indica il valore massimo assunto dalla densità di probabilità Pmax nel
caso di una rete con 100,000 neuroni, in presenza di disordine annealed. (b) Andamento del campo P̄ in funzione di Ē, al variare delle dimensioni della rete. In
entrambi le figure si ha una diluizione del 20% ed inoltre α = 9, g = 0.4 e a = 1.3.
la figura (4.12a), vediamo non solo che le curve P (v) diventano più localizzate al
crescere di N, ma anche che la struttura delle curve varia all’aumentare delle dimensioni della rete. In figura (4.12a) è riportato inoltre l’andamento della densità
di probabilità P (v) per una rete con N = 100,000 neuroni, in presenza di disordine
annealed. Tale curva appare come la curva limite per la densità di probabilità calcolata in presenza di disordine quenched. Nell’inserto è mostrato l’andamento dei
valori massimi assunti dalla densità di probabilità Pmax in funzione di N; tali valori
aumentano all’aumentare della dimensione della rete e sembrano saturare al valore
massimo assunto dalla densità di probabilità stimata per una rete di N = 100,000
neuroni con disordine annealed.
Per caratterizzare lo stato collettivo del sistema riportiamo, nel piano (Ē, P̄ ),
l’attrattore corrispondente (figura 4.12b). All’aumentare delle dimensioni della rete
le curve si allargano e il loro spessore si assottiglia e sembrano convergere ad una
curva limite, riportata in figura e corrispondente ad una rete di N = 100,000 neuroni, con disordine annealed. Il caso con disordine quenched sembra cosı̀ convergere
a quello con disordine annealed nel limite termodinamico. Questa congettura, che il
limite termodinamico dei sistemi con disordine quenched sia rappresentato da quelli
con disordine annealed, è confermata, oltre che dai risultati riportati in figura (4.12),
anche dall’analisi dell’andamento del valore massimo assunto da Ē in funzione del
numero di neuroni nella rete. Come mostrato in figura (4.13a), tale valore tende ad
un valore asintotico al crescere di N; l’asintoto è rappresentato dal valore massimo
del campo Ē ottenuto nel caso di disordine annealed per N = 100,000 neuroni.
Per verificare quantitativamente se le fluttuazioni di Ē tendono a svanire nel limite
termodinamico, stimiamo la sua deviazione standard σ
7
su una serie di misure suc-
cessive. Dalla figura (4.13b) si osserva un decadimento di σ con una legge a potenza
del tipo N −ζ con ζ = 0.52 ± 0.02. Questo risultato è assolutamente non ovvio, dato
che σ non rappresenta l’errore sulla media Ē, ma la larghezza della distribuzione dei
valori assunti istantaneamente dai campi {Ei }, quindi ci dice che nel limite termodinamico i campi si sincronizzano tutti fra di loro. Il fatto che l’esponente con cui
decade σ sia prossimo ad 1/2 ci suggerisce che gli scarti osservati fra i vari campi
abbiano un’origine di tipo stocastico. In effetti ogni campo Ei , ad un determinato
7
Indicando con H il numero di potenziali d’azione emessi nell’intervallor
di tempo considerato, la
PN
P
P
Ek2 (tj )
H
H
1
1
k=1
deviazione standard riportata è definita come σ = H j=1 σj = H j=1
− Ē 2 (tj ).
N
istante, è dato dalla sovrapposizione lineare di impulsi che hanno raggiunto il neurone i a tempi diversi. Quindi, questi impulsi avranno ampiezze differenti al tempo
considerato ed il campo si può quindi vedere come una sovrapposizione lineare di
variabili stocastiche. Assumendo che gli impulsi di ampiezza rilevante per il campo abbiano raggiunto il neurone in un intervallo di tempo unitario, precedente al
tempo in esame, è facile mostrare che il loro numero è proporzionale ad N. Quindi
ci possiamo aspettare dal teorema del limite centrale8 , assumendo la decorrelazione
degli impulsi, che nel limite N → ∞, i campi Ei siano distribuiti in modo gaussiano
√
con una deviazione standard che decresce come 1/ N .
0.1
2.2
max E
2.1
2
σ
0.01
1.9
1.8
1.7
1.6
(b)
(a)
100
1000
10000
N
0.001
100
1000
10000
N
Figura 4.13. (a) Andamento del valore massimo assunto dal campo Ē al variare
delle dimensioni della rete. È riportato inoltre il valore limite a cui tali campi
dovrebbero convergere nel limite termodinamico. Il valore limite è dato dal massimo di Ē, trovato con disordine annealed. L’asse delle ascisse è riportata in scala
logaritmica. Il valore massimo di Ē è stato calcolato considerando, a seconda del
valore di N , da 104 sino a 106 iterazioni della mappa ad evento guidato che corrispondono, per ogni N , a 3100 punti di massimo. (b) Andamento della deviazione
standard del campo Ē in funzione delle dimensioni della rete. Entrambi gli assi
sono, in questo caso, in scala logaritmica. La deviazione standard ha un andamento stimato pari a σ ∝ N −ζ con ζ = 0.52 ± 0.02. Il numero di impulsi emessi
nell’intervallo di tempo considerato, su cui viene eseguita la media temporale per
σ, è pari a H = 900. In entrambe le figure si ha una diluizione del 20% ed inoltre
α = 9, g = 0.4 e a = 1.3.
Stimiamo ora il grado di caoticità del sistema attraverso il calcolo dell’ esponente
di Lyapunov massimo per varie taglie del sistema. Riportiamo in figura (4.14) l’andamento dell’esponente di Lyapunov massimo λ1 in funzione delle dimensioni della
8
Il teorema del limite centrale afferma che la somma di un un numero Z sufficientemente alto
di variabili indipendenti e aleatorie, ognuna con varianza e media finite, sarà distribuita come una
gaussiana con la stessa media delle variabili originarie e varianza ridotta di un fattore Z.
√
rete. Nonostante le fluttuazioni di Ē decrescano come 1/ N , λ1 rimane positivo al
crescere di N e tende a saturare verso un valore asintotico, anch’esso diverso da zero
e positivo, entro le barre di errore 9 . Una stima del valore a cui tende l’esponente
di Lyapunov massimo nel limite N → ∞ si ottiene dall’interpolazione dei dati a
N ≥ 6400 con un andamento del tipo A + B/ ln(N) ed in particolare dal valore
dell’intercetta A. Si ha cosı̀ che il valore asintotico stimato è λ1 = (12 ± 1) · 10−2.
L’andamento logaritmico con N di λ1 si può collegare a quanto trovato per sistemi
caotici a molti gradi di libertà, con accoppiamento diffusivo, quali le mappe accoppiate [38, 39], ove è stato visto che l’esponente di Lyapunov massimo del sistema
varia rispetto all’esponente della singola mappa caotica in maniera inversamente proporzionale al valore assoluto del logaritmo della costante di accoppiamento; questo
si osserva per accoppiamenti sufficientemente piccoli. Occorre notare che, nel caso presente, la costante di accoppiamento è proporzionale a 1/N, come si deduce
dall’espressione per l’accoppiamento impulsivo (4.3, 4.4).
Dunque, nonostante i campi Ei si sincronizzino tra loro e la dinamica macroscopica, caratterizzata dal campo Ē, tenda a divenire periodica, il sistema resta
caotico nel limite N → ∞. Questo indica chiaramente che il caos, in questo caso,
ha un’origine microscopica nella dinamica dei singoli potenziali di membrana. È importante notare che questa situazione è altamente non banale. Questa si può vedere
come una generalizzazione dello stato parzialmente sincronizzato in reti globalmente
connesse ad una situazione in cui la dinamica dei singoli neuroni è diversa a causa
del disordine presente nella rete.
9
Le barre di errore sono state calcolate prendendo dieci diverse realizzazioni della rete su cui
calcolare, in maniera indipendente, λ1 e la deviazione standard tra questi valori.
0.1
0.08
0.06
λ1
0.04
y= A + B/ ln N
0.02
0
0
5000
10000
15000
20000
25000
30000
N
Figura 4.14. Andamento dell’esponente di Lyapunov massimo λ1 in funzione di N .
La curva tratteggiata magenta rappresenta l’interpolazione ottimale dei dati con
6400 ≤ N ≤ 25600 con una curva del tipo y = A + B/ ln(N ), con A = 0.12 ± 0.01
e B = −0.24 ± 0.04. Le simulazioni effettuate si riferiscono ad una rete con il 20%
di legami recisi, α = 9, g = 0.4 e a = 1.3.
4.5
Disordine annealed
Caratterizziamo in questo paragrafo la dinamica della rete ad α = 9 in presenza
di disordine annealed; il disordine della rete viene adesso generato ad ogni passo
di evoluzione della mappa, quindi la presenza (o l’assenza) dei legami tra i neuroni
viene ridefinita ad ogni passo di integrazione. Per brevità non riportiamo, in questo
paragrafo, i risultati numerici relativi all’analisi dello scenario di biforcazione in presenza di disordine annealed, dato che qualitativamente otteniamo gli stessi risultati
trovati nel paragrafo (4.3) in presenza di disordine quenched. Ci concentriamo invece sull’analisi della dinamica microscopica e macroscopica della rete, alla stregua
di quanto fatto nel paragrafo precedente.
Analizzando la densità di probabilità P (v), osserviamo, analogamente al caso di
disordine quenched, curve sempre più localizzate all’aumentare delle dimensioni del
sistema. Ma, mentre nel caso di reti con disordine quenched variava sia la forma
della curva che l’altezza del picco, nel caso presente la forma della curva non cambia
sostanzialmente all’aumentare delle dimensioni della rete. Questa è un’indicazione
800
1600
3200
6400
25000
50000
100000
15
16
Pmax
14
10
12
P(v)
0
20000
40000
60000
80000
10
1e+05
N
5
0
0
0.2
0.4
v
0.6
0.8
1
Figura 4.15. Andamento della densità di probabilità P (v) in funzione del potenziale di membrana v, al variare delle dimensioni della rete. Nell’inserto mostriamo
l’andamento del valore assunto dalla densità di probabilità in corrispondenza del
massimo, Pmax , al variare di N . Nell’inserto non sono riportate le barre di errore perché risultano minori dei simboli impiegati. Le simulazioni effettuate si
riferiscono ad una rete con il 20% di legami recisi, α = 9, g = 0.4 e a = 1.3.
della maggior omogeneità della rete anche a valori bassi di N. Inoltre, data la localizzazione sempre maggiore delle curve mostrate in figura (4.15), ci aspettiamo,
anche in questo caso, di avere una sincronizzazione completa nel limite termodinamico. Questo è confermato da quanto riportato nell’inserto della figura (4.15), dove
mostriamo l’andamento crescente del valore assunto da P (v) in corrispondenza del
picco, al variare di N.
Analizziamo adesso l’attrattore associato alla dinamica macroscopica (figura
4.16), caratterizzato dalle curve riportate nel piano (Ē,P̄ ) per vari N. Nel caso
presente si osserva una modesta modifica della forma delle curve, che si allargano in
modo relativamente ridotto al crescere delle dimensioni della rete, mentre si osserva
sempre una diminuzione delle fluttuazioni delle curve con N, come ci si aspettava da
quanto riportato al paragrafo precedente. In altri termini le ampiezze massime dei
campi Ē e P̄ variano poco all’aumentare di N e si osserva solo una diminuzione dello
spessore degli attrattori, che convergono ad una curva limite per N → ∞, come è
36
P
35
1600
6400
25000
100000
34
0.9
1
1.1
1.2
1.3
(b)
1.4
1.5
E
Figura 4.16. Entrambe le figure mostrano l’andamento del campo P̄ in funzione
di Ē, al variare delle dimensioni della rete. (a) Sono riportate le curve complete
nel piano (Ē,P̄ ), per sette diverse dimensioni della rete. (b) In questo caso la
figura mostra un particolare ingrandito delle curve mostrate in (a); i risultati delle
simulazioni interessano, in questo caso solo quattro diverse dimensioni della rete,
per maggior chiarezza. In entrambi i casi si ha una diluizione del 20% ed inoltre
α = 9, g = 0.4 e a = 1.3.
ben visibile in figura (4.16b), dove abbiamo ingrandito una piccola zona degli attrattori mostrati in figura (4.16a), nell’intorno del massimo di Ē. Si deduce dunque
l’esistenza di una curva limite, che è identica, sia per il caso di disordine quenched,
che per quello annealed. In altri termini, i due sistemi sembrano convergere ad
un’unica curva nel limite termodinamico.
La generazione aleatoria delle connessioni attive tra i neuroni ad ogni passo di
evoluzione della mappa comporta, per il sistema, la capacità di automediarsi. È
lecito supporre dunque che le fluttuazioni tra i campi dei singoli neuroni siano più
piccole nel caso di disordine annealed rispetto al caso di disordine quenched. Le
800
800, E
3200
3200, E
50000
50000, E
2.5
2
1.5
E
1
0.5
(a)
0
4525
4530
4535
4540
4545
4550
Tempo
Figura 4.17. Andamento di un campo E di singolo neurone e del campo Ē in funzione del tempo. Le simulazioni sono state eseguite per differenti dimensioni della
rete; in particolare i risultati riportati interessano reti con N = 800, 3200, 50,000
neuroni. Inoltre si ha una diluizione del 20%, α = 9, g = 0.4 e a = 1.3.
fluttuazioni nel caso presente sono effettivamente piccole, come si vede in figura
(4.17). Qui confrontiamo infatti l’andamento del campo Ei dell’i-esimo neurone
con il campo medio Ē, per diverse taglie del sistema. Anche per la taglia più
piccola (N = 800 neuroni) si nota che la differenza tra il campo del singolo neurone
e quello mediato su tutti i neuroni è minima; questo significa che vi è una forte
sincronizzazione fra tutti i campi Ei .
Le fluttuazioni tendono a svanire nel limite N → ∞. Questo è riscontrabile
anche attraverso l’ulteriore analisi riportata in figura (4.18), dalla quale si ricava
che il campo Ē satura ad un valore fissato al crescere di N e che la larghezza della
distribuzione dei campi {Ei }, quantificata ad ogni istante dalla deviazione standard
σ definita nel paragrafo precedente, tende a zero al crescere di N come N −ζ , con
ζ = 0.51 ± 0.01, come mostrato in figura (4.18b). Questo risultato indica che le
fluttuazioni dei campi si comportano in modo analogo a quanto riportato per il
caso di disordine quenched. In figura (4.18a) viene mostrato l’andamento del valore
massimo assunto da Ē in funzione della dimensione della rete. Diversamente dal
caso di disordine quenched, in cui il valore massimo di Ē sembrava saturare ad
0.1
2.28
2.27
max E
2.26
σ
2.25
0.01
2.24
2.23
(a)
2.22
1000
10000
N
1e+05
(b)
0.001
100
1000
10000
1e+05
N
Figura 4.18. (a) Andamento del valore massimo assunto dal campo Ē al variare
delle dimensioni della rete. L’asse delle ascisse è riportata in scala logaritmica. Il
valore massimo di Ē è stato calcolato considerando, a seconda del valore di N ,
da 104 sino a 106 iterazioni della mappa ad evento guidato che corrispondono,
per ogni N , a 3100 punti di massimo. (b) Andamento della deviazione standard
del campo Ē in funzione delle dimensioni della rete. La deviazione standard è
stata calcolata secondo la formula riportata nel paragrafo precedente. Entrambi
gli assi sono, in questo caso, in scala logaritmica. La stima dell’andamento della
deviazione standard è σ ∝ N −ζ , con ζ = 0.51±0.01. Il numero degli impulsi emessi
nell’intervallo di tempo considerato, su cui si effettua la media temporale per σ,
è pari a H = 900. In entrambe le figure si ha una diluizione del 20% ed inoltre
α = 9, g = 0.4 e a = 1.3.
un valore costante solo nel limite N → ∞, nel caso di disordine presente il valore
massimo sembra saturare ad un valore fissato già per N = 25,000.
Caratterizziamo ora la dinamica del sistema attraverso il calcolo degli esponenti
di Lyapunov massimi per varie taglie della rete. L’andamento di questo indicatore
è ciò che differenzia maggiormente il caso di disordine quenched da quello annealed.
Infatti, nonostante la dinamica del campo Ē per i sistemi con disordine quenched
tenda a saturare verso quella per sistemi con disordine annealed, si ha un diverso
andamento di λ1 nel limite N → ∞. Facendo riferimento alla figura (4.19) vediamo
che, nel caso di disordine annealed, l’esponente di Lyapunov massimo sembra tendere
a zero nel limite N → ∞ con un andamento del tipo 1/ ln N. In questo caso
abbiamo evidenze numeriche che il sistema diventi periodico e riacquisti le proprietà
dinamiche del sistema globalmente accoppiato nel limite termodinamico
10
10
.
Anche nel caso presente le barre di errore sono calcolate utilizzando 10 configurazioni iniziali
diverse della rete e 10 risultati diversi dell’esponente di Lyapunov massimo su cui calcolare la
deviazione standard. Le barre di errore sono più piccole rispetto al caso precedente dal momento
che la variazione delle configurazioni iniziali della rete influisce meno sul proseguo della simulazione
nel caso di disordine annealed rispetto al caso di disordine quenched. Nel caso di disordine annealed
Possiamo osservare che il decadimento a zero come 1/ ln N dell’esponente di
Lyapunov massimo è stato osservato anche in sistemi di particelle autogravitanti globalmente accoppiate [40]. In tali sistemi il campo autoconsistente a cui sono
soggette le particelle fluttua irregolarmente, mentre nel caso di reti diluite con disordine annealed il campo Ē sembra avere un andamento periodico nel limite N → ∞.
Dal momento che le particelle autogravitanti in questione sono indistinguibili, possiamo considerare il fatto che entrambi i sistemi presentino lo stesso andamento
dell’esponente di Lyapunov massimo in funzione di N, come una chiara indicazione
dell’effetto di omogeneizzazione degli accoppiamenti visti dai vari neuroni, introdotto
dal disordine annealed. In altri termini questo ci fa supporre che una rete diluita con
disordine annealed si comporti come una rete globalmente accoppiata ed omogenea
nel limite termodinamico.
0.03
(a)
0.025
0.02
λ1 0.015
0.01
0.005
0
0
10000
5000
N
Figura 4.19. Andamento dell’esponente di Lyapunov massimo in funzione di N .
Sono riportati i risultati delle simulazioni effettuate con disordine annealed in scala
lineare. Le simulazioni effettuate si riferiscono ad una rete con il 20% di legami
recisi, α = 9, g = 0.4 e a = 1.3.
le connessioni vengono comunque rigenerate ad ogni passo di evoluzione della mappa, quindi la
condizione iniziale pesa molto di più nelle reti con disordine quenched, visto che rimane fissata per
tutto il tempo di evoluzione della mappa.
4.6
Confronto con il sistema globalmente accoppiato
Come riportato nel paragrafo precedente la generazione del rumore annealed è tale
da indurre, di fatto, una omogeneizzazione degli accoppiamenti visti dai vari neuroni
quindi, nel limite N → ∞, ci possiamo aspettare che una rete diluita, con disordine
annealed, si comporti dinamicamente come una rete omogenea con un termine di
accoppiamento ridotto della percentuale di diluizione dei legami.
Chiariamo ora in maggiore dettaglio come l’accoppiamento entri nella dinamica
di ogni singolo neurone. Come si nota dall’equazione (3.4), il termine forzante che
regola la dinamica del neurone è gE(t), quindi ci aspettiamo che due reti con uguali
termini forzanti (g Ē, g P̄ ) abbiano la stessa dinamica, qualora tutti i campi siano
sufficientemente sincronizzati.
Per prima cosa verifichiamo se, per una rete omogenea ad α fissato, cambiare il
parametro di accoppiamento g non equivalga ad un banale riscalamento dei campi
(Ē,P̄ ). Consideriamo il caso α = 9; in questo caso sappiamo, dal diagramma di fase
(3.3), che a gc = 0.42±0.02 si ha una transizione da uno stato asincrono ad uno stato
parzialmente sincronizzato. Come confermato dall’analisi della densità di probabilità
P (v) riportata in figura (4.20a), per g > gc la densità di probabilità è pressoché
uniforme, mentre si presenta sempre più localizzata per g < gc , al diminuire di g.
Se riportiamo invece gli attrattori per vari valori di g, con le ampiezze riscalate
del valore dell’accoppiamento corrispondente (figura 4.20b) vediamo che le curve
cambiano forma e non è possibile sovrapporre una curva all’altra. Quindi variare
l’accoppiamento ad α costante vuol dire modificare strutturalmente l’attrattore e la
dinamica del neurone corrispondente.
Cerchiamo adesso di verificare l’ipotesi fatta, secondo la quale vi è corrispondenza
0.20
0.24
0.28
0.32
0.36
0.40
0.44
0.48
0.52
30
P(v) 20
10
(a)
0
0
0.2
0.4
v
0.8
0.6
1
Figura 4.20. (a) Andamento della densità di probabilità P (v) in funzione del
potenziale di membrana v. Facendo riferimento al diagramma di fase (3.3) descritto
nel paragrafo (3.2.3), sappiamo che si ha una transizione dallo stato parzialmente
sincronizzato allo stato asincrono in corrispondenza di gc = 0.42 ± 0.02 per il
valore di α utilizzato. Questa transizione si può notare anche in figura, dove si
passa da una distribuzione piccata ad una uniforme tra g = 0.40 e g = 0.44. (b)
Andamento del campo riscalato gP̄ in funzione del campo riscalato gĒ al variare
della costante di accoppiamento g. Le varie curve sono dunque riscalate per la
costante di accoppiamento corrispondente. Le simulazioni effettuate si riferiscono
ad una rete globalmente connessa con N = 1600 neuroni, α = 9 e a = 1.3.
15
10
gP
5
0
0
0.2
0.4
0.6
0.8
1
gE
Figura 4.21. Andamento del campo riscalato gP̄ in funzione del campo riscalato
gĒ. La curva azzurra è il risultato della simulazione del comportamento di una
rete globalmente connessa con N = 1600 neuroni, con parametri α = 9, a = 1.3
e g = 0.32. In questo caso i campi Ē, P̄ sono moltiplicati dunque per g = 0.32.
La curva nera è il risultato delle simulazioni effettuate considerando una rete di
100,000 neuroni, in presenza di disordine annealed e di una percentuale di legami
rotti pari al 20%. In questo secondo caso i parametri in gioco sono α = 9, a = 1.3
e g = 0.4, dunque i campi Ē, P̄ sono moltiplicati per g = 0.4.
tra sistemi con disordine annealed e sistemi omogenei con parametro d’accoppiamento ridotto della percentuale di diluizione. A tal fine riportiamo in figura (4.21) le
variabili medie che caratterizzano il campo (Ē, P̄ ), moltiplicate per il termine di
accoppiamento g, sia per una rete globalmente accoppiata con g = 0.32, che per una
rete con disordine annealed ed il 20% di legami rotti ma con g = 0.4. Si osserva che
queste due curve si sovrappongono perfettamente. Quindi possiamo concludere che,
almeno nel caso di disordine annealed, la rete si comporta come una rete omogenea
globalmente accoppiata con un accoppiamento ridotto in modo opportuno.
4.7
Neuroni disaccoppiati guidati dalla rete
L’omogeneità indotta dalla media sul disordine annealed fa sı̀ che il sistema risulti
esattamente omogeneo nel limite N → ∞ quindi, come nel caso di reti globalmente
accoppiate, l’esponente di Lyapunov massimo tende a zero. D’altra parte, nonostante l’analogia strutturale che permane tra una rete con disordine quenched ed una
globalmente accoppiata, abbiamo visto che l’attrattore rimane caotico all’aumentare
di N. Cerchiamo dunque di capire quali siano le ragioni per cui si realizza tale dinamica caotica e l’origine del caos. In particolare cerchiamo di capire se un sistema
come quello da noi studiato, descritto dall’equazione (4.1), possa dar luogo ad una
situazione caotica o meno nell’eventualità in cui il campo autoconsistente, forzante
Ei (t) venga sostituito da un campo periodico E(t) uguale per tutti i neuroni. Occorre sottolineare il fatto che la dinamica del singolo neurone i è caratterizzata da
tre gradi di libertà (vi ,Ei ,Pi ), quindi in linea di principio potremmo avere caos [33].
Per generare un campo periodico, il più simile possibile a quello generato autoconsistentemente dalla rete diluita con disordine annealed, ma ripulito dalle fluttuazioni
dovute alla diluizione e a N finito, abbiamo mediato il campo Ē non solo su tutti
i neuroni della rete ad ogni passo di evoluzione della mappa, ma anche su finestre
temporali successive riscalando opportunamente l’ampiezza delle finestre temporali.
Spieghiamo più in dettaglio come viene generato il campo cui saranno soggetti i
neuroni della nostra indagine. Abbiamo preso il campo Ē calcolato per una rete di
N = 800 neuroni, in presenza di disordine annealed ed abbiamo stimato il periodo
medio di oscillazione T di tale campo. In particolare indichiamo con T la media di
tutti gli intervalli di tempo intercorsi tra un massimo ed il successivo del campo Ē.
Analizziamo adesso il segnale Ē in funzione del tempo tra un punto di massimo ed
il successivo, suddividendolo cosı̀ in finestre temporali. Per ogni finestra temporale
riscaliamo la scala dei tempi indipendentemente in modo che ogni periodo abbia
valore T . Campioniamo poi il campo Ē ad intervalli regolari dt, in modo da ottenere
sempre un numero di punti Np fissato entro ogni finestra temporale. In particolare
abbiamo scelto Np = 1024. In altri termini, per ogni finestra temporale, otteniamo
un campo campionato a passi temporali dt, con dt = T /Np . D’altra parte Ē è stato
calcolato ad ogni passo di aggiornamento della mappa e dunque sarà registrato ad
intervalli di tempo non costanti e non necessariamente pari a dt. Occorre ricordare
infatti che gli aggiornamenti della mappa avvengono in concomitanza dell’emissione
di un impulso ed il tempo di evoluzione della rete è dato dalla somma dei tempi che
intercorrono tra un’emissione e la successiva di un impulso. Dunque per ottenere
i nuovi valori del campo Ē a passi di tempo regolari a partire da quelli registrati
abbiamo effettuato un’interpolazione lineare. Se indichiamo con Nf il numero di
finestre temporali analizzate, il campo desiderato sarà quello risultante dall’ulteriore
media sulle Nf finestre.
Ci troviamo a questo punto a lavorare con un campo definito in un intervallo
temporale [0, T ], mediato su tutti i neuroni della rete ad ogni istante e su finestre
temporali successive. Se indichiamo con Ē(t˜k ) il campo Ē campionato a tempi
equispaziati, il nuovo campo sarà definito da
< Ē(t˜k ) >=
PNf
˜
j=1 Ēj (tk )
Nf
k = 1, · · · ,Np .
(4.23)
In figura (4.22a) riportiamo sia l’andamento in funzione del tempo del campo Ē
calcolato per la rete di N = 800 neuroni con disordine annealed, sia l’andamento
1
2
0.8
E, <E>
1.5
0.6
v
1
0.4
0.2
0.5
0
(a)
0.5
1
1.5
2
2.5
Tempo
(a)
10
5
15
Tempo
Figura 4.22. (a) Andamento del campo medio Ē in funzione del tempo (curva
nera). Tale campo medio è prodotto da una rete guida costituita da N = 800 neuroni, in presenza di disordine annealed e con il 20% di legami rotti. A questa curva
sovrapponiamo il campo < Ē > ottenuto mediando non solo sui singoli neuroni
della rete ad ogni istante di tempo, ma anche su finestre temporali successive (curva rossa); tale campo è campionato inoltre in modo temporalmente equispaziato.
(b) Andamento di due potenziali di membrana in funzione del tempo. Anche se
i due potenziali partono con condizioni iniziali diverse, con il passare del tempo,
si sincronizzano tra loro. Le simulazioni effettuate utilizzano i seguenti valori dei
parametri per la rete guida: g = 0.4, α = 9 e a = 1.3.
del campo mediato anche su finestre temporali successive opportunamente riscalate.
Occorre notare innanzitutto quanto il campo < Ē > sia simile al campo autoconsistente Ē generato dalla rete diluita nell’intervallo di tempo comune [0, T ]. Inoltre
il nuovo campo < Ē > è ripulito dalle fluttuazioni presenti nel campo Ē, specie
nelle zone di minimo, dovute al disordine provocato dalla diluizione. Se ripetiamo
su intervalli temporali successivi [T, 2T ], [2T, 3T ], · · · ,[(Nf − 1)T, Nf T ] il campo
< Ē > trovato, otteniamo il campo periodico cercato.
Una volta ottenuto questo segnale ne abbiamo calcolato la trasformata di Fourier
in modo da ottenere tutti i coefficienti della sua decomposizione in serie di Fourier.
Questo allo scopo di poter rigenerare il segnale ad ogni tempo e non solo ai tempi
campionati. Abbiamo bisogno infatti di un campo noto a tutti i tempi per usarlo
come campo forzante per la dinamica di più neuroni disaccoppiati al fine di studiare
la sincronizzazione dei neuroni fra di loro e col campo esterno.
Per vedere se un campo siffatto può indurre comportamenti caotici, abbiamo
utilizzato il campo < Ē > come campo esterno per forzare un sistema di due neuroni
disaccoppiati. Il sistema di equazioni differenziali del primo ordine indipendenti che
descrive il sistema è dato da
v̇i = a − vi + g < Ē(t) >
i = 1,2.
(4.24)
Tale sistema è stato integrato numericamente utilizzando l’algoritmo Runge-Kutta
del quarto ordine11 con passo temporale 5 · 10−4 [41]. Ai neuroni considerati vengono
assegnati, come condizioni iniziali, due valori diversi per i potenziali di membrana.
Nonostante ciò, nel corso della loro evoluzione temporale si osserva che i due neuroni si sincronizzano tra loro, molto rapidamente, come è visibile in figura (4.22b).
Dopo la sincronizzazione, analizzando i tempi tra un’emissione e la successiva di un
potenziale d’azione da parte dei singoli neuroni, si ricava che tali tempi coincidono
con il periodo T del campo forzante. Dunque non solo i neuroni si sincronizzano tra
loro, ma si sincronizzano anche con il campo esterno.
Abbiamo più volte ripetuto che il campo < Ē > approssima al meglio campi non
periodici, quali sono i campi Ē prodotti da una rete diluita con disordine annealed.
A questo punto due neuroni sottoposti allo stesso campo si sincronizzano rapidamente. Ciò dimostra che le differenze tra i campi Ei dei singoli neuroni in grandi
reti e le fluttuazioni presenti nel campo Ē, seppur piccole, sono molto importanti
nell’evoluzione dinamica di una rete ed inducono caos nel sistema
12
. Dunque le
dinamiche caotiche osservate nel caso di disordine annealed, ad N finiti, sono da
imputarsi alle fluttuazioni, seppur minime, nella periodicità delle diverse variabili
microscopiche Ei , Pi associate ai vari neuroni nella rete. Addirittura queste fluttuazioni sono talmente rilevanti nel caso quenched da indurre la presenza di caos
anche nel limite termodinamico.
11
Per calcolare con esattezza gli attraversamenti di soglia e i successivi riazzeramenti del potenziale abbiamo adottato una tecnica con passo temporale adattivo.
12
Infatti va ricordato che, anche nel caso con disordine annealed, per N finito, il sistema è pur
sempre caotico.
Conclusioni
L’attività di ricerca originale descritta in questa tesi ha avuto come scopo quello di
caratterizzare vari regimi dinamici collettivi che emergono, spontaneamente, in reti
neurali con accoppiamento eccitatorio impulsivo.
In particolare si è confrontata la dinamica di reti omogenee e reti diluite di
neuroni leaky integrate-and-fire al fine di dedurre quali segnature degli stati coerenti,
osservati in reti globalmente connesse, permanessero in presenza di diluizione e quali
differenze insorgessero. La diluizione delle connessioni della rete è stata realizzata
in modo aleatorio, con l’introduzione di due diversi tipi di disordine: congelato
(“quenched”) o generato dinamicamente (“annealed”).
Per quel che riguarda le reti globalmente accoppiate, un primo risultato consiste nell’aver mostrato, attraverso analisi numeriche accurate, che gli spettri di
Lyapunov, ottenuti per diverse taglie del sistema, collassano su una curva universale, se opportunamente riscalati, sia in regime di stato asincrono che in regime di
sincronizzazione parziale. Tale risultato comporta che entrambi gli stati divengono
marginalmente stabili nel limite termodinamico e ci suggerisce che l’introduzione di
un minimo disordine nel sistema possa influenzare la stabilità di tali stati macroscopici. Se verificato, questo porrebbe seri limiti sulla rilevanza di queste soluzioni
collettive per la codifica dell’informazione in reti neurali.
Per indagare la stabilità rispetto al disordine di questi stati, abbiamo quindi
esaminato cosa accade introducendo diluizioni aleatorie nel sistema. Per prima cosa
abbiamo osservato che il sistema diviene caotico, mentre la dinamica delle variabili
macroscopiche si svolge su attrattori caotici localizzati in prossimità delle soluzioni
regolari del sistema non disordinato. Inoltre, al crescere del numero di elementi nella
rete, la localizzazione aumenta, indicando una notevole stabilità strutturale degli
attrattori associati alle oscillazioni collettive rispetto all’introduzione di disordine
sia quenched che annealed nella distribuzione delle connessioni.
L’analisi della dipendenza dell’esponente di Lyapunov massimo dal numero N
di neuroni nella rete per le due differenti realizzazioni del disordine ha evidenziato
come nel caso annealed l’esponente tenda a zero nel limite termodinamico, mentre
resti finito nel caso quenched. Questo suggerisce che nel caso annealed la continua
ridefinizione dinamica delle connessioni porti di fatto ad una loro omogeneizzazione.
Quindi nel limite N → ∞ ci aspettiamo che la dinamica del sistema diluito converga a quella del sistema completamente connesso, come in effetti si è verificato,
confrontando l’attrattore ottenuto nel caso di diluizione annealed con quello del caso
omogeneo, per cui l’accoppiamento sia stato opportunamente rinormalizzato.
Nel caso di reti con disordine quenched permangono alcune segnature tipiche
dell’analisi di campo medio: si osserva ad esempio che a livello macroscopico il
limite termodinamico dei sistemi con disordine quenched è rappresentato da quelli
con disordine annealed. Dunque, nonostante i campi forzanti visti dai singoli neuroni
tendano a sincronizzarsi tra di loro e a divenire periodici, la dinamica microscopica
resta manifestamente caotica, dato che l’esponente di Lyapunov massimo tende a
saturare ad un valore costante.
Questo risultato, oltre a non essere mai stato riportato in letteratura, è altamente
non banale e per certi versi sorprendente. Come mostrato in questa tesi, l’origine di
questa dinamica caotica va ricercata nelle minime differenze che permangono fra i
campi associati ad ogni singolo neurone e che sono indotte dalla struttura congelata
(quenched) delle connessioni aleatorie. Per i limiti temporali in cui una tesi deve
necessariamente svolgersi, una comprensione completa del fenomeno è rimandata a
futuri sviluppi del lavoro di ricerca su questo tema.
In conclusione, possiamo affermare che gli stati parzialmente sincronizzati risultano robusti rispetto all’introduzione di disordine nelle connessioni. Questa stabilità strutturale li rende particolarmente adatti alla trasmissione di informazione,
che potrebbe ad esempio essere codificata nel periodo del segnale macroscopico [42],
dato che in reti reali, quali quelle cerebrali, la presenza di rumore esogeno ed endogeno è inevitabile. La rilevanza di dinamiche coerenti, quali quelle rappresentate
dagli stati parzialmente sincronizzati, per la comunicazione neuronale, è stata recentemente messa in luce da P. Fries [43] analizzando la sincronizzazione dell’attività
neuronale nella banda γ in molte aree della corteccia cerebrale e dell’ippocampo.
Questi risultati rappresentano un punto di partenza per poter affrontare problematiche più complesse, quali la dinamica di reti maggiormente realistiche, in cui
i singoli neuroni siano rappresentati da modelli fisiologicamente rilevanti e dove i
pesi sinaptici possano modificarsi nel tempo rispecchiando le evidenze sperimentali
di fenomeni di plasticità sinaptica e di ritardo.
È importante menzionare infine che, per lo svolgimento di questo lavoro di tesi,
il candidato ha sviluppato codici originali in linguaggio C, al fine di effettuare le
simulazioni numeriche riportate in precedenza.
Appendice A
Fenomenologia delle biforcazioni
Una biforcazione identifica un cambiamento nel comportamento dinamico di un
sistema quando uno o più parametri di biforcazione passano attraverso un valore
critico. Ogni punto nello spazio dei parametri dove il sistema è strutturalmente
instabile
1
è un punto di biforcazione e l’insieme di tali punti è chiamato un insieme
di biforcazione. Alcuni sistemi mostrano anche un’isteresi, ossia la biforcazione
avviene per differenti valori dei parametri a seconda della direzione in cui sono
variati. Esistono molti modi di classificare le biforcazioni:
• in base alla dimensione del sistema, ossia al numero di variabili dinamiche;
infatti alcune biforcazioni esistono solo quando la dimensione supera un valore
minimo ed è sufficiente analizzare la biforcazione nella minima dimensione in
cui si verifica in quanto niente di fondamentalmente nuovo è aggiunto dalle
dimensioni più alte;
• in base alla codimensione della biforcazione, ossia al numero dei parametri in
conseguenza della cui variazione si ha la biforcazione;
• biforcazioni locali e globali ; nelle prime i punti fissi appaiono, scompaiono
1
Un sistema è detto strutturalmente instabile quando piccole variazioni dei valori dei parametri
portano a modifiche radicali del suo spazio delle fasi e quindi della sua dinamica.
109
o cambiano la loro stabilità; le seconde invece sono dovute a interazioni fra
attrattori diversi, o fra i loro bacini di attrazione (la distinzione tra i due
tipi tuttavia non è sempre ovvia poiché ci sono biforcazioni con entrambe le
caratteristiche);
• biforcazioni continue (o sovra-critiche) e discontinue (o sotto-critiche) come
andremo nel seguito ad illustrare.
In questa trattazione noi considereremo solo biforcazioni locali di codimesione-1.
A.1
Biforcazioni sovra-critiche di punti fissi
I matematici hanno dimostrato che sotto condizioni piuttosto generali il comportamento locale di biforcazioni di codimensione-1 da un punto fisso può essere ridotto a
poche caratteristiche essenziali. Più precisamente è stato provato che esistono espansioni in serie e cambi di variabile tali che, vicino ad un punto fisso, il comportamento
è descritto da un piccolo numero di equazioni differenziali che dipendono da un solo parametro µ [44, 45]. Intuitivamente questo sembra ragionevole per biforcazioni
di codimensione-1. Dopo aver effettuato opportune trasformazioni di variabili che
portano il punto fisso nell’origine x = 0 ed il punto di biforcazione nel punto µ = 0
le equazioni della dinamica assumono forme caratteristiche dette forme normali del
tipo:
ẋ = f (x,µ)
(A.1)
dove f (x,µ)î (con î versore dell’asse x) è il vettore che rappresenta il campo di flusso.
Limitandoci al terzo ordine descriveremo brevemente le quattro forme normali più
spesso incontrate.
1) Biforcazione sella-nodo: ẋ = µ − x2 .
Se µ < 0 l’equazione f (x,µ) = 0 non ha soluzioni reali e perciò non ci sono
punti fissi. Se µ = 0 ci sono due soluzioni coincidenti nel punto x = 0 entrambe
instabili. Le due soluzioni si separano quando µ > 0: in tal caso si ha una
√
√
soluzione stabile, x = + µ, ed una instabile, x = − µ (vedi fig.A.1A).
2) Biforcazione transcritica: ẋ = µx − x2 .
In questo caso si hanno due punti fissi, x = 0,µ, la cui stabilità cambia quando
il parametro di biforcazione attraversa il valore critico µ = 0: per µ < 0 si ha
che x = 0 è stabile e x = µ è instabile, viceversa per µ > 0 (vedi fig.A.1B).
3) Biforcazione a forcone: ẋ = µx − x3 .
Se µ ≤ 0 si ha un solo punto fisso stabile in x = 0. Se µ > 0 si ha una
√
biforcazione in tre punti fissi: x = 0 che diventa instabile e x = ± µ che
invece sono stabili (vedi fig.A.1C).
4) Biforcazione di Hopf : ż = (µ + iγ)z − z|z|2 .
In questa forma normale z è una variabile complessa e γ è una costante che
comunque non ha il ruolo di parametro di biforcazione. Questa forma normale
è l’equivalente complesso di quella della biforcazione a forcone. Per trovare
la soluzione è conveniente trasformarla in variabili reali usando coordinate
cartesiane o polari. Ponendo z = x + iy la forma normale diviene:
ẋ = [µ − (x2 + y 2 )]x − γy
(A.2)
ẏ = γy + [µ − (x2 + y 2 )]y.
(A.3)
A parte la soluzione z = 0 (ossia x = y = 0) esiste un’altra soluzione:
|z|2 = (x2 + y 2 ) = µ
la quale definisce un cerchio di raggio
√
µ nel piano (x,y).
(A.4)
Dunque per µ ≤ 0 si ha un unico punto fisso stabile in x = y = 0; mentre per
µ > 0 esso diventa instabile e contemporaneamente si ha la nascita di un ciclo limite
stabile (vedi fig.A.1D).
Figura A.1. Diagramma di biforcazioni sovracritiche: A) sella-nodo; B) transcritica; C) forcone; D) Hopf. La linea continua indica i punti stabili mentre le linee
tratteggiate indicano i punti instabili. Le frecce rappresentano inoltre la direzione
delle linee di forza del campo di flusso f (x,µ)î (dove î è il versore dell’asse x) [44].
A.2
Biforcazioni sotto-critiche
Le forme normali considerate al paragrafo A.1 sono dette sovra-critiche (o normali ).
Con questo intendiamo che i termini non lineari in x2 e x3 hanno un effetto opposto a quello dell’instabilità causata dal termine di ordine più basso. Prendiamo ad
esempio la forma ẋ = µx − x3 . Per x molto piccolo possiamo considerare solo il
termine lineare. La soluzione che si ottiene è allora x = exp(µt), che diverge all’infinito quando µ è positivo. Ma la soluzione dell’intera equazione non diverge
esponenzialmente perché il termine lineare è controbilanciato dal termine (−x3 ) che
cresce rapidamente in modo cosı̀ grande da non poter essere trascurato. Ponendo
l’equazione nella forma:
ẋ = µx(1 −
x2
)
µ
(A.5)
vediamo che il termine non lineare “satura” l’effetto dell’instabilità lineare quando
x2 = µ. Comunque niente proibisce che il termine non lineare di ordine più basso abbia anche un’influenza destabilizzante sulla soluzione. La biforcazione in questo caso
è chiamata sotto-critica o inversa. Tutte le forme normali esaminate al paragrafo
A.1 possono essere rese sotto-critiche semplicemente cambiando il segno del termine
non lineare. Otteniamo cosı̀ i diagrammi di biforcazione presentati in fig.A.2.
Figura A.2. Diagramma di biforcazioni sottocritiche (o inverse): A) sella-nodo;
B) transcritica; C) forcone; D) Hopf. La linea continua indica i punti stabili mentre
le linee tratteggiate indicano i punti instabili. Le frecce rappresentano inoltre la
direzione delle linee di forza del campo di flusso f (x,µ)î (dove î è il versore dell’asse
x) [44].
Appendice B
Metodo della sezione di Poincaré
L’evoluzione di numerosi sistemi è descritta da un insieme di n equazioni differenziali
ordinarie del primo ordine:
d
x(t) = F(x,t),
dt
(B.1)
dove x è un vettore in Rn (lo spazio delle fasi) e F è un campo vettoriale definito
su questo spazio. Un sistema di equazioni differenziali come quello descritto da
(B.1) è detto flusso in Rn . Se F non dipende esplicitamente dal tempo ma solo da
x, F = F (x(t)), il flusso è detto autonomo. Le soluzioni dell’insieme di equazioni
(B.1) hanno un’espressione analitica solo in situazioni ben definite in cui il flusso è
integrabile. Nella maggior parte dei casi il flusso non è integrabile ed occorre studiare
ciascuna soluzione considerando la sua traiettoria nello spazio delle fasi. Possiamo
semplificare questa analisi usando un metodo sviluppato da Henri Poincaré.
B.1
Mappa di Poincaré
In teoria non ci sono restrizioni alla dimensione n dello spazio delle fasi, ma ci limiteremo, per semplicità, al caso tridimensionale. Piuttosto che studiare le soluzioni
dell’insieme (B.1) in R3 , può essere utile considerare i punti di intersezione della
traiettoria con un piano S. La costruzione è indicata in figura (B.1). Abbiamo
114
Figura B.1. Principio della sezione di Poincaré. La traiettoria Γ taglia il piano S
con la condizione ẋ3 < 0 nei punti P0 , P1 , P2 ,...Questi appartengono alla sezione
di Poincaré di Γ sul piano S. [44].
definito tale piano come x3 = costante e abbiamo preso i punti dell’intersezione che
corrispondono ad una data direzione dell’evoluzione (ẋ3 < 0). L’altezza h del piano
è scelta in modo che la traiettoria Γ intersechi S in P0 , P1 , P2 ,· · ·. A partire da una
data condizione iniziale otteniamo un insieme di punti che costituiscono la sezione
di Poincaré.
La trasformazione che porta da un punto al successivo è una mappatura continua
T : S → S chiamata mappa di Poincaré:
Pk+1 = T(Pk ) = T(T(Pk−1 )) = T2 (Pk−1 ) = · · · .
(B.2)
Dal momento che la soluzione dell’insieme di equazioni (B.1) è unica, il punto P0
determina completamente P1 , che a sua volta determina P2 e cosı̀ via. D’altra parte
se P1 determina univocamente P0 , semplicemente invertendo il segno di t nell’insieme
(B.1), allora T è una mappatura invertibile di S in se stessa.
Notiamo che la sezione di Poincaré sostituisce l’evoluzione a tempo continuo
dell’insieme (B.1) con una trasformazione a tempo discreto. In genere l’intervallo
di tempo tra due punti successivi non è costante. Infine occorre sottilineare che la
sezione e la mappa di Poincaré hanno, per costruzione, le stesse proprietà topologiche
del flusso da cui derivano. Ad esempio, se il flusso è dissipativo, cosicché i volumi
nello spazio delle fasi si contraggono, allora T contrae le aree nel piano S. Invece T
conserva le aree se il flusso (B.1) è conservativo o Hamiltoniano. Allo stesso modo,
se il flusso ha un attrattore, le sue caratteristiche strutturali sono riscontrabili anche
nella sezione di Poincaré.
Il metodo della sezione di Poincaré semplifica lo studio dei flussi continui sostanzialmente per tre motivi. Innanzitutto, se passiamo da un flusso in R3 ad una mappatura sul piano, riduciamo di uno il numero di coordinate. Inoltre il tempo è discretizzato e le equazioni differenziali vengono sostituite con le equazioni che definiscono la
mappa di Poincaré P → T(P ). Queste equazioni algebriche sono più facili da risolvere. Infine la quantità di dati da manipolare si riduce notevolmente, dal momento
che la maggior parte dei punti della traiettoria vengono ignorati. Dunque iterare
una mappatura del piano xi (k + 1) = T(xi (k)), i = 1,2, è molto più semplice che
integrare un flusso del tipo (B.1), sia in termini di tempo che di potenza di calcolo.
B.2
Sezioni di Poincaré per differenti attrattori
Quando la soluzione di un insieme di equazioni differenziali è periodica, la traiettoria
nello spazio delle fasi è un’orbita chiusa, il ciclo limite. La corrispondente sezione
di Poincaré è molto semplice, dal momento che si riduce ad un singolo punto P0 ,
o ad un numero finito di punti nell’eventualità che il ciclo limite abbia una forma
complicata. Questo punto costituisce un punto fisso della mappa di Poincaré T
poiché
P0 = T(P0 ) = T2 (P0 ) = · · · .
(B.3)
Grazie a questa proprietà è possibile investigare la stabilità della soluzione periodica.
Discutiamo dunque della stabilità di una traiettoria chiusa rispetto alle perturbazioni
infinitesime; in questo caso è sufficiente un’analisi di stabilità lineare limitata a
termini del primo ordine nella perturbazione. La mappa di Poincaré è descritta, al
primo ordine, da una matrice DT definita nell’intorno di P0 da:
"
∂T
DT =
∂xi
#
i = 1,2.
(B.4)
x0i
La matrice, chiamata matrice di Floquet, permette di stimare la distanza dell’immagine di un punto P0 + δ, molto vicino a P0 , calcolata dopo un periodo:
T(P0 + δ) − P0 ≃ DTδ
||δ|| → 0.
(B.5)
Gli autovalori di DT determinano la stabilità della traiettoria. Dopo m periodi si
ha
Tm (P0 + δ) − P0 ≃ DTm δ
(B.6)
cosicché la distanza iniziale δ è moltiplicata per DTm . La distanza decresce esponenzialmente nel tempo se gli autovalori di DT hanno tutti modulo minore di 1, ovvero
se sono tutti contenuti nel cerchio unitario del piano complesso. In questo caso la
traiettoria periodica è linearmente stabile, dal momento che qualsiasi allontanamento dal punto fisso tende ad annullarsi. D’altra parte, se almeno un autovalore di DT
ha modulo maggiore di 1, l’allontanamento dal punto fisso cresce esponenzialmente
nel tempo ed il ciclo limite diventa instabile. La perdita di stabilità del ciclo limite
corrisponde ad avere uno o più autovalori della matrice di Floquet che attraversano
il cerchio unitario nel piano complesso.
Quando la soluzione è biperiodica, con due frequenze fondamentali f1 e f2 , l’attrattore è un toro T 2 che può essere rappresentato in R3 . Qualsiasi traiettoria sulla
superficie del toro può essere vista come una sovrapposizione di due moti (vedi figura B.2). Ciascuna frequenza fondamentale f1 , f2 è associata con uno di questi moti
rotazionali. I punti di intersezione di una traiettoria con un piano di sezione S
appaiono ad intervalli di tempo regolari, pari al periodo del primo moto (in questo
Figura B.2. Toro T 2 e la sua sezione di Poincaré col piano S. Le due frequenze
con cui il toro è percorso sono indicate come f1 e f2 . Assunto che il rapporto f1 /f2
risulti irrazionale, la sezione di Poincaré corrispondente è la curva chiusa C. [44].
caso T1 = 1/f1 ). I punti si collocano su una curva chiusa C; la forma esatta della
sezione di Poincaré dipende dal rapporto f1 /f2 . Se questo rapporto è irrazionale, la
traiettoria non si chiude mai su se stessa e copre in maniera densa la superficie del
toro; in questo caso le due frequenze sono dette incommensurabili. La curva chiusa
C è continua. dal momento che ciascuno dei suoi punti costituisce l’immagine, sotto
T, di un altro punto di C, la curva è invariante sotto la mappatura T:
T(C) = C.
(B.7)
Quando il rapporto f1 /f2 è razionale, la sezione di Poincaré è composta da un insieme
finito di punti distribuiti lungo C. La curva C non è più una curva continua, dal
momento che la traiettoria non è densa sul toro. C’è un agganciamento in frequenza
tra f1 e f2 : il rapporto f1 /f2 è uguale a quello di due interi n1 e n2 . Dopo aver
effettuato n1 circuiti ed n2 rotazioni la traiettoria si richiude su se stessa dal momento
che abbiamo a che fare con una soluzione periodica di periodo T = (n1 /f1 ) =
(n2 /f2 ). La sezione di Poincaré contiene solo n1 punti, cosicché
Pi = Tn1 (Pi ).
(B.8)
Analizziamo infine il caso di soluzione aperiodica. Quando il flusso è molto
dissipativo e si ha una rapida contrazione delle aree, la sua sezione di Poincaré
può essere considerata come un insieme di punti distribuiti lungo una curva. In
questo caso si definisce una coordinata x per ciascun punto della curva e si studia
come x vari con il tempo. La mappa di Poincaré su questa curva è detta mappa
di primo ritorno. Un’estensione naturale dello studio della sezione di Poincaré è
dunque l’analisi della mappa di primo ritorno, ovvero dell’iterazione xk+1 = f (xk ),
che esprime la relazione tra le coordinate di un punto e quelle del suo antecedente.
Appendice C
Stabilità lineare
C.1
Stabilità lineare di orbite periodiche: moltiplicatori di Floquet
Consideriamo un sistema di equazioni differenziali del primo ordine dx/dt = F(x),
dove x è un vettore di Rn e F è un campo vettoriale definito in Rn . Studiamo la
stabilità lineare di un’orbita periodica definita come
x(t) = X∗ (t) = X∗ (t + T ),
(C.1)
dove T denota il periodo. Senza perdita di generalità si può assumere che l’orbita
periodica verifichi la relazione F (X∗ ) = 0. Vogliamo esaminare il comportamento
delle orbite vicino a X∗ (t), per cui poniamo
x(t) = X∗ (t) + η(t),
(C.2)
dove assumiamo che la perturbazione η sia piccola. Sostituendo l’equazione precedente nel sistema di equazioni dx/dt = F(x) ed espandendo F(x) al primo ordine
in η si ha
F(X∗ (t) + η(t)) = F(X∗ (t)) + DF(X∗ ) · η + O(η 2 ),
120
(C.3)
dove F(X∗ ) = 0 essendo valutato sull’orbita periodica, mentre DF denota la matrice
Jacobiana delle derivate parziali di F. Otteniamo cosı̀ che
dη/dt = DF(X∗ (t)) · η + O(η 2 ),
(C.4)
dove DF(X∗ (t)) varia periodicamente nel tempo. Trascurando i termini di ordine
η 2 nell’equazione (C.4) ci si riduce ad uno studio di stabilità lineare della forma
dy/dt = A(t) · y,
(C.5)
dove y è un vettore reale N-dimensionale ed A(t) è una matrice N × N a coefficienti
reali e periodica nella variabile temporale,
A(t) = A(t + T ).
(C.6)
Le soluzioni dell’equazione (C.5) possono essere espresse nella forma di Floquet,
e(t)e(s+iϕ)t , dove e(t) è periodico nel tempo: e(t) = e(t + T ). Possiamo definire cosı̀
un problema agli autovalori per gli autovalori sj e per gli autovettori ej (t).
Innanzitutto notiamo che l’equazione (C.4) ha una soluzione che corrisponde ad
un autovalore con parte reale nulla (s = 0). Questo si può verificare differenziando
rispetto al tempo l’equazione dX∗ (t)/dt = F(X∗ (t)). Questo ci permette di ottenere un’equazione della forma (C.5), ovvero de0 (t)/dt = DF(X∗ (t)) · e0 (t), dove
e0 ≡ dX∗ /dt. Questa soluzione con autovalore s = 0 corrisponde ad una perturbazione η(t) lungo la direzione dell’orbita periodica in esame. Tale perturbazione
non decadrà nè divergerà nel tempo.
Implementiamo adesso il metodo di sezione di Poincaré per ridurre il problema
dx/dt = F(x) ad una mappa x̂n+1 = M(x̂n ). Assumiamo che la soluzione periodica
X∗ (t) risulti un punto fisso x̂∗ della mappa. Linearizzando la mappa attorno ad x̂∗
e scrivendo x̂n = x̂∗ + η̂ n , con η̂ n piccolo, si ottiene
η̂ n = DM(x̂∗ ) · η̂ n + O(η̂ 2n ),
(C.7)
che dà un problema linearizzato della forma
ŷn+1 = Â · ŷn .
(C.8)
Cercando le soluzioni ŷ = µn ê, otteniamo l’equazione agli autovalori del tipo
Â · ê = µê.
(C.9)
Questa equazione ha soluzioni non banali per quei valori di µj che soddisfano l’equazione polinomiale
D̂(µ) = det[Â − µI] = 0.
(C.10)
Agli autovalori µj facciamo corrispondere gli autovettori êj . Le direzioni che corrispondono a |µj > 1| sono instabili; le direzioni che corrispondono a |µj < 1| sono
stabili. Gli autovalori della mappa e gli autovalori di Floquet sono legati dalla
relazione
µj = exp(sj T ),
(C.11)
dove sono inclusi tutti gli sj del problema di Floquet eccetto l’autovalore nullo.
Quest’ultimo non è incluso poiché una perturbazione η che sposta l’orbita lungo il
cammino chiuso seguito da X∗ (t) non contribuisce a perturbazioni lungo la sezione di
Poincaré, che tipicamente taglia il flusso in modo ortogonale al senso di percorrenza
dell’orbita.
C.2
Esponenti di Lyapunov
Dal momento che non è possibile seguire il moto su un attrattore caotico a causa
della divergenza esponenziale di orbite vicine, dobbiamo utilizzare altri strumenti per
caratterizzare questa divergenza. Questo può essere fatto introducendo i cosiddetti
esponenti di Lyapunov che costituiscono la generalizzazione degli autovalori di un
punto fisso (o ciclo limite) della teoria di Floquet.
Consideriamo innanzitutto il caso di una mappa M. Sia x0 una condizione
iniziale e sia xn l’orbita corrispondente dopo n iterate. Se consideriamo uno spostamento infinitesimo da x0 in direzione di un vettore tangente y0 , allora l’evoluzione
del vettore tangente, data da
yn+1 = DM(xn ) · yn ,
(C.12)
determinerà l’evoluzione dello spostamento infinitesimo dell’orbita dall’orbita imperturbata xn . In particolare, yn /|yn | dà la direzione dello spostamento infinitesimo
dell’orbita da xn , mentre |yn |/|y0 | rappresenta il fattore di crescita o di descrescita
dello spostamento infinitesimo dopo n iterate, a seconda che |yn | sia maggiore o
minore di |y0 |. Dall’equazione (C.12) si ricava inoltre che yn = DMn (x0 ) · y0 , dove
DMn (x0 ) = DM(xn−1 )DM(xn−2 ) · · · DM(x0 ).
(C.13)
è la matrice di evoluzione nello spazio tangente relativa alla n-esima iterata. Definiamo cosı̀ l’esponente di Lyapunov per una condizione iniziale x0 e per una data
direzione dello spostamento iniziale u0 = y0 /|y0 | come
λ(x0 ,y0 ) = lim
n→∞
1
1
ln(|yn |/|y0 |) = lim ln |DMn (x0 ) · u0 |.
n→∞ n
n
(C.14)
Se la dimensione della mappa è N ci aspettiamo di trovare, per un dato x0 , un
numero di esponenti di Lyapunov distinti minore o uguale ad N. Ciascuno di questi
esponenti dipende dalla direzione di u0 .
Per capire perché, in linea di principio, sono possibili valori diversi degli esponenti di Lyapunov che dipendono dall’orientazione di u0 , approssimiamo l’espressione
(C.14) supponendo di avere un n sufficientemente grande. In questa approssimazione
λ(x0 ,u0 ) ≃ λ̄n (x0 ,u0 ) ≡
=
1
ln |DMn (x0 ) · u0 |
n
(C.15)
1
ln[u†0 · Hn (x0 ) · u0 ],
2n
dove Hn (x0 ) = [DMn ]† DMn (x0 ) e † indica la trasposta. Dal momento che Hn (x0 )
è una matrice hermitiana reale non negativa, ha autovalori reali e possiamo scegliere
gli autovalori in modo che siano reali. Supponendo che u0 giaccia nella direzione di
un autovettore di Hn (x0 ), otteniamo come valori per l’esponente di Lyapunov approssimato quelli che corrispondono a ciascun autovettore. Denotiamo questi valori
λ̄jn (x0 ) = (2π)−1 ln Hjn , dove Hjn identifica un autovalore di Hn (x0 ). Ordiniamo
gli indici dei {λ̄jn (x0 )} in modo che λ̄1n (x0 ) ≥ λ̄2n (x0 ) ≥ · · · ≥ λ̄N n (x0 ). In questo
modo λ̄1n (x0 ) è l’esponente più grande, mentre λ̄N n (x0 ) è il più piccolo. Se effettuiamo il limite n → ∞, i {λ̄jn (x0 )} tendono al valore degli esponenti di Lyapunov,
per cui varrà
λ1 (x0 ) ≥ λ2 (x0 ) ≥ · · · ≥ λN (x0 ).
(C.16)
Dunque se scegliamo u0 in modo arbitrario, questo potrà essere decomposto nella
somma delle componenti lungo gli autovettori
u0 =
N
X
aj ej ,
(C.17)
j=1
dove con ej identifichiamo gli autovettori ortonormali di Hn (x0 ). Si ottiene cosı̀ che
u†0 · Hn (x0 ) · u0 =
N
X
a2j exp[2nλ̄jn (x0 )].
(C.18)
j=1
Per n sufficientemente grandi, il termine dominante nella somma è quello che corrisponde a j = 1, ovvero quello che corrisponde all’autovalore massimo,
u†0 · Hn (x0 ) · u0 ≃ a1 exp[2nλ̄1n (x0 )].
(C.19)
Dunque una scelta arbitraria di u0 nell’equazione (C.14) fa sı̀ che venga selezionato
solo l’autovalore massimo λ1 (x0 ). Per ottenere λ2 (x0 ) occorre restringere u0 al
sottospazio ortogonale a e1 ; questo equivale a porre a1 = 0. Si ottiene cosı̀
u†0 · Hn (x0 ) · u0 ≃ a2 exp[2nλ̄2n (x0 )].
(C.20)
Procedendo in questo modo si possono ottenere tutti gli esponenti di Lyapunov.
L’implementazione numerica richiede comunque tecniche di calcolo particolari; analizzeremo una di queste tecniche nel paragrafo (C.2.1).
Se assegnamo le condizioni iniziali in una sfera di raggio infinitesimo δ, centrata
in x0 e lasciamo evolvere ciascuna condizione iniziale secondo la mappa M, si ottiene
che, in un tempo n, essa evolve in un ellissoide di semi-assi:
δi ≃ δenλi (x0 ,n)
i = 1, · · · ,N.
(C.21)
Nel limite n → ∞ gli esponenti di Lyapunov danno il tasso temporale di crescita o
di decrescita degli assi principali dell’ellissoide.
Infine si può dimostrare che, sotto specifiche ipotesi, gli esponenti di Lyapunov
assumono lo stesso insieme di valori per determinati x0 . Infatti il teorema ergodico
di Osedelec [46] garantisce l’esistenza dei limiti usati per definire gli esponenti di
Lyapunov sotto ipotesi molto generali. In particolare, se µ è una misura ergodica,
i valori degli esponenti λi (x0 ) ottenuti a partire dalle equazioni (C.12,C.14) sono
gli stessi per tutti gli x0 rispetto alla misura µ. Nel caso della misura naturale
sull’attrattore, questo implica che gli esponenti di Lyapunov rispetto a tale misura
assumono lo stesso insieme di valori per tutti gli x0 che si trovano nel bacino di
attrazione dell’attrattore, tranne che per un insieme di misura di Lebesgue nulla.
Possiamo dunque parlare di esponenti di Lyapunov di un attrattore senza far riferimento alle specifiche condizioni iniziali. Definiamo cosı̀ un attrattore caotico se ha
un esponente di Lyapunov positivo. In questo caso due condizioni iniziali a distanza
infinitesima tra loro si separano esponenzialmente nel tempo (ad ogni modo se le
condizioni iniziali giacciono su un attrattore limitato, la separazione esponenziale
varrà solo per distanze piccole rispetto alla dimensione dell’attrattore).
C.2.1
Tecnica di calcolo numerico degli esponenti di Lyapunov
Una tecnica per il calcolo numerico degli esponenti di Lyapunov per orbite caotiche
è stata introdotta da Benettin et al. [34]. Consideriamo innanzitutto il calcolo dell’esponente massimo λ1 . Scegliamo in maniera arbitraria y0 , in modo che abbia una
componente nella direzione di massima crescita esponenziale. Iterando l’equazione
(C.12) per un tempo lungo, |yn | diventa tipicamente cosı̀ grande da non poter essere
calcolabile numericamente se λ1 > 0. Tale problema può essere superato rinormalizzando periodicamente |y| a 1. In altri termini, scegliamo arbitrariamente un
intervallo di tempo τ e rinormalizziamo il vettore tangente dividendolo per il suo
modulo αj ad ogni tempo τj = jτ . Se memorizziamo gli αj , l’esponente di Lyapunov
massimo può essere stimato come
l
1 X
ln αj .
l→∞ lτ
j=1
λ1 = lim
(C.22)
Scegliendo un l sufficientemente grande, affinché il risultato numerico risulti rilassato
ad un valore costante, possiamo approssimare l’espressione per λ1 come
l
1 X
λ1 ≃
ln αj .
lτ j=1
(C.23)
Per calcolare il secondo esponente di Lyapunov scegliamo due vettori iniziali arbitrari
(1)
e indipendenti y0
(2)
e y0 . Questi vettori identificano l’area A0 in due dimensioni
di un parallelogramma che giace in uno spazio delle fasi N-dimensionale. Iterando
questi due vettori n volte, si ottengono i vettori yn(1) e yn(2) che identificano un
(1)
parallelogramma di area An . Assumendo che y0
e y02 abbiamo componenti non
nulle nelle direzioni e1 ed e2 , il parallelogramma di partenza viene distorto, dopo n
iterazioni, e la sua area diventa An ∼ exp[n(λ1 + λ2 )]A0 . Abbiamo cosı̀ che
λ1 + λ2 = n→∞
lim
1
ln(An /A0 ).
n
(C.24)
Quindi, data una stima numerica di λ1 , tramite il calcolo numerico del membro di
destra dell’equazione precedente possiamo avere una stima numerica anche per λ2 .
Ci sono comunque due difficoltà: (1) come in precedenza, yn(1) e yn2 tendono a diventare molto grandi al crescere di n; (2) la loro orientazione tende a coincidere. Per
risolvere questi problemi occorre estendere la tecnica di calcolo di λ1 , generalizzando
la procedura di normalizzazione. Ad ogni tempo τj occorre sostituire la coppia di
vettori che evolvono, con una coppia di vettori ortonormalizzati nello spazio lineare
a due dimensioni in cui si estendono i vettori non ortonormalizzati di partenza.
Otteniamo cosı̀
l
1 X
(2)
λ1 + λ2 ∼
ln αj ,
=
lτ j=1
(2)
dove αj
(C.25)
è l’area del parallelogramma, prima della normalizzazione, al tempo τj .
Per gli esponenti λk (k = 3,4, · · ·) successivi la procedura è la stessa. Facciamo
evolvere k vettori, memorizzando il volume del parallelepipedo k-dimensionale che
essi definiscono, e rinormalizziamo l’insieme dei k vettori ad ogni tempo τj . In questo
caso ad ogni tempo τj sostituiamo i vettori non normalizzati con il corrispondente
insieme di vettori ortonormali definiti attraverso la procedura di ortonormalizzazione
di Gram-Schmidt. Tale procedura preserva il sottospazio lineare sotteso dai vettori
evoluti prima della normalizzazione. Otteniamo dunque
k
X
l
1 X
(k)
λk ′ ≃
ln αj ,
lτ j=1
k ′ =1
(C.26)
(k)
dove αj è il volume del parallelepipedo k-dimensionale prima della normalizzazione.
Sottraendo il risultato per k − 1 da quello per k si ottiene
l
1 X
(k)
(k−1)
∼
λk =
ln(αj /αj
),
lτ j=1
valido per k ≥ 2.
(C.27)
C.2.2
Dimensione dell’attrattore
È stata congetturata da parte di Kaplan e Yorke [47] l’esistenza di una relazione tra
la dimensione frattale di un tipico attrattore caotico e gli esponenti di Lyapunov.
Prima di analizzare tale relazione introduciamo la matrice
1
T (x0 ) = lim [Hn (x0 )] 2n .
(C.28)
n→∞
Indichiamo con E la dimensione nello spazio delle fasi del vettore x0 e con Ek (x0 ) il
sottospazio di RE corrispondente agli autovalori di T (x0 ) che sono ≤ eλk . Gli esponenti di Lyapunov ci danno, nell’approssimazione lineare, la rapidità di espansione o
contrazione media lungo le traiettorie modo crescente. Dunque, il sottospazio E1 /E2
consiste di tutti i vettori e nello spazio tangente a Mn che crescono con rapidità
massima, mentre i vettori in E2 /E3 di quelli che evolvono con esponente pari a λ2 ,
etc. Allora un vettore infinitesimo in RE diverge esponenzialmente concordemente
al moltiplicatore h1 = enλ1 , in un tempo n; un elemento di superficie invece cresce
come h1 h2 = en(λ1 +λ2 ) . Ma dato che il sistema è dissipativo, considerando elementi
di dimensione crescente, prima o poi si trova un indice j tale che
ma
Pj+1
k=1
Pj
k=1 λk
≥ 0,
λk < 0. Questo significa che gli elementi di dimensione j sono ancora
espansi o conservati, ma quelli a dimensione più alta vengono contratti; possiamo
dedurne, ricordando il significato di dimensione come numero di variabili attive, che
la dimensione dell’attrattore sarà maggiore o uguale a j. La relazione esatta tra
la dimensione frattale e gli esponenti di Lyapunov (congettura di Kaplan-Yorke) è
data da
Dky = j +
dove j è l’indice più grande e
Pj
k=1 λk
Pj
k=1 λk
|λj+1|
,
≥ 0. Ricordando che
(C.29)
Pj
k=1
λk ci dà la velocità
di crescita del volume j-dimensionale, nello spazio tangente, si vede subito che l’equazione (C.29) non è altro che l’interpolazione lineare per ottenere l’indice j ∗ per
cui la quantità
Pj ∗
k=1
λk si annulla. Questa relazione è ormai verificata in un’ampia
casistica e conserva sempre il significato di limite superiore per la dimensione frattale. Dky è detta dimensione di Lyapunov o di Kaplan-Yorke.
Bibliografia
[1] L. Peliti, Appunti di meccanica statistica, Bollati Boringhieri (2003).
[2] J.J. Hopfield, Neural networks and physical systems with emergent
selective computational abilities, Proc. Natl. Acad. Sci. USA 79, 2554
(1982).
[3] D.J. Amit, Modeling brain function. The world of attractor neural
networks, Cambridge University Press (1989).
[4] S. Maya, R. Reynoso, C. Torres e M. Arias-Estrada, Compact Spiking Neural Network Implementation in FPGA, Lecture Notes in Computer Science
1896, 270 (2000).
[5] L.F. Abbott e C. van Vreeswijk, Asynchronous states in networks of
pulse-coupled oscillators, Phys. Rev. E 48, 1483 (1993).
[6] P.K. Mohanty e A. Politi, A new approach to partial synchronization in
globally coupled rotators, J. Phys. A: Math. Gen. 39, L415 (2006).
[7] C. Allene et al., Sequential Generation of Two Distinct Synapse-Driven
Network Patterns in Developing Neocortex, The Journal of Neuroscience
26, 12851 (2008).
[8] C. Koch, Biophysics of computation, Oxford University Press, New York
(1999).
[9] P. Dayan e L.F. Abbott, Theoretical Neuroscience: Computational and
Mathematical Modeling of Neural Systems, The MIT Press, Cambridge
(2001).
[10] R. Zillmer, R. Livi, A. Politi e A. Torcini, Stability of splay state in pulsecoupled networks, Phys. Rev. E 76, 046102 (2007).
[11] D.Z. Jin, Fast convergence of spike sequences to periodic patterns in
recurrents networks, Phys. Rev. Lett. 89, 208102 (2002).
130
[12] R. Zillmer, R. Livi, A. Politi e A. Torcini, Desynchronization in diluted
neural networks, Phys. Rev. E 74, 036203 (2006).
[13] S. Ramón y Cayal, Histologie du Système Nerveux de l’Homme et des
Vertébré, A. Maloine, Parigi (1909).
[14] J.G. Nicholss, R.A. Martin e B.G. Wallace, Dai Neuroni al cervello,
Zanichelli, Bologna (1997).
[15] W. Gerstner e W. Kistler, Spiking Neuron Models, Cambridge University
Press, Cambridge (2002).
[16] M.N. Shadlen e W.T. Newsome, The variable discharge of cortical neurons: implications for connectivity, computation, and information
coding, J. Neurosci. 18, 3870 (1998).
[17] D.K.S. Smetters, Electrotonic structure and synaptic integration in cortical neurons, Massachusetts Institute of Technology: Cambridge, Massachusetts (1995).
[18] D. Johnston e S. Miao-Sin Wu, Foundations of Cellular Neurophysiology,
Massachusetts Institute of Technology: Cambridge, Massachusetts (1995).
[19] S.G. Cull-Candy, R. Miledi e I. Parker, Single glutamate-activated channels recorded from locust muscle fibres with perfused patch-clamp
electrodes, J. Physiol. 321, 195 (1980).
[20] E.R. Kandel, J.H.Schwartz e T.M. Jessell, Principles of neural science,
McGraw-Hill (2000).
[21] K. Huang, Statistical mechanics, John Wiley & Sons, New York (1987).
[22] D.E. Goldman, Potential, impedance and rectification in membranes,
J. Gen. Physiol. 342, 37 (1943).
[23] A.L. Hodgkin e B. Katz, The efffect of sodium ions on the electrical
activity of the giant axon of the squid, J. Physiol. 108, 37 (1949).
[24] L.J. Mullins e K. Noda, The influence of sodium-free solutions on membrane potential of frog muscle fibers, J. Gen. Physiol. 47, 117 (1963).
[25] A.L. Hodgkin e A.F. Huxley, Currents carried by sodium and potassium
ion throught the membrane of the giant axon of Loligo, J. Physiol. 116,
449 (1952).
[26] A.L. Hodgkin e A.F. Huxley, A quantitative description of membrane
current and its application to conduction and excitation in nerve, J.
Physiol. 117, 500 (1952).
[27] L. Lapicque, Recherches quantitatives sur l’excitation electrique des
nerfs traitee comme une polarization, J. Physiol. Pathol. Gen. 9, 620
(1907).
[28] A. Destexhe, Z.F. Mainen, T.J. Sejnowski, An Efficient Method for Computing Synaptic Conductances Based on a Kinetic Model of Receptor
Binding, Neural Computation 6, 14 (1994).
[29] C. van Vreeswijk, Partial synchronization in populations of pulsecoupled oscillators, Phys. Rev. E 54, 5522 (1996).
[30] R. Kapral, R. Livi, G.L. Oppo e A. Politi, Unpredictable behaviour in
stable systems, Europhys. Lett. 22, 571 (1993).
[31] F. Ginelli, R. Livi, A. Politi e A. Torcini, Relationship between directed
percolation and the synchronization transition in spatially extended
systems, Phys. Rev. E 67, 046217 (2003).
[32] A. Politi e A. Torcini, Stable Chaos, In fase di stampa, arXiv:0902.2545
(2009).
[33] E. Ott, Chaos in dynamical systems, Cambridge University Press (1993).
[34] G. Benettin et al., Lyapunov Characteristic Exponents for smooth dynamical systems and for hamiltonian systems; a method for computing all of them. Part 1: Theory, Meccanica 9, 21 (1980).
[35] I. Shimada e T. Nagashima, A numerical approach to ergodic problem
of dissipative dynamical systems, Prog. Theor. Phys. 61, 1605 (1979).
[36] L.M. Pecora e T.L. Carroll, Synchronization in chaotic systems, Phys.
Rev. Lett. 64, 821 (1990).
[37] A. Pikovsky, M. Rosenblum, J. Kurths, Synchronization: a universal concept in nonlinear sciences, Cambridge University Press, Cambridge (2003).
[38] R. Livi, A. Politi e S. Ruffo, Scaling law for the maximal Lyapunov exponent , J. Phys. Math. Gen. 25, 4813 (1992).
[39] A. Torcini, R. Livi, A. Politi e S. Ruffo, Comment on “universal scaling
law for the largest Lyapunov exponent in coupled map lattices”, Phys.
Rev. Lett. 78, 1391 (1997)
[40] H. Chate, F. Ginelli, K.A. Takeuchi, A. Politi e A. Torcini, Lavoro in fase di
realizzazione (2009). .
[41] W.H. Press, S.A. Teukolsky, W.T. Vetterling e B. P. Flannery, Numerical
recipes in C, Cambridge University Press (1992).
[42] G. Buzsáki, Rhythms of the brain, Oxford University Press (2006).
[43] P. Fries, A mechanism for cognitive dynamics: neuronal communication through neuronal coherence, Trends in Cognitive Sciences 9(10), 474
(2005).
[44] P. Bergé, Y. Pomeau e C. Vidal, Order within chaos, Herman e John Wiley
& Sons, Parigi (1984).
[45] J. Clinton Sprott, Chaos and Time-Series Analysis, Oxford University
Press, New York (2003).
[46] V.I. Osedelec, A multiplicative ergodic theorem. Lyapunov characteristic numbers for dynamical systems, Moscow Math. Soc. 19, 197 (1968).
[47] J.L. Kaplan e J.A. Yorke, Chaotic behavior of multidimensional difference equations in ”Functional Differential Equations and Approximation of Fixed Points”, Lect. Not. Math. 13, 730 (1979).
Ringraziamenti
Innanzitutto esprimo la mia gratitutide, per l’ospitalità e la collaborazione fornitami, all’Istituto dei Sistemi Complessi (I.S.C.) del Consiglio Nazionale delle Ricerche
(C.N.R.), dove è stato svolto questo lavoro di tesi, ed in particolare al prof. Antonio Politi. Sono in debito nei confronti del dott. Giampiero Puccioni per le
innumerevoli consulenze e del dott. Alessandro Torcini per i continui suggerimenti.
Debbo ringraziare inoltre per la collaborazione e le utili discussioni avute il mio
relatore prof. Roberto Livi. Infine voglio sottolineare che questa tesi è stata resa
possibile grazie al sostegno e all’affetto della mia famiglia.
134